Y''+4xy'+(2+4x^2)y=0 дифф урав решать?
Другие вопросы по теме Алгебра
Популярные вопросы
- Сравните особенности светской российской системы образования с традиционной...
2 - Какие счета бухгалтерского учета открывают для учета собственного...
2 - Дано: у1=45 у26 = -5 найти: d = ? у20 = ?...
2 - Технология. В чем заключается окончательная отделка изделия? (ответить...
3 - 4) Watch the video again with sound. Completethe paragraph with...
2 - Сколько будет 555999555*666999666...
3 - очень Окончания имен прилагательных после шипящих и ц 1. Переписать,...
2 - 10. Установите правильное соответствие: 1) 1223 г. а) Ледовое побоище...
2 - Алые паруса в учебнике, составьте цитатный план этого отрывка (с....
1 - А1. Найдите производную функции: И вычисли ее значение в точке х=1...
3
Если дифференциальное уравнение представлено в форме
Это замена формы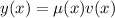
Положим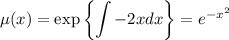 и подставив замену
и подставив замену 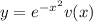 , получим
, получим
Возвращаемся к обратной замене