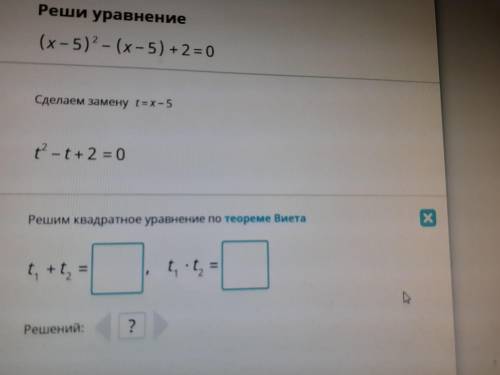
(x-5)²-(x-5)+2=0 Сделаем замену t=x-5
t²-t+2=0
Решим квадратное уравнение по теореме Виета
t¹+t²=_ t¹×t²=_
Решений _
И нужно записать ответ для t чему равно, и чему равен x
Другие вопросы по теме Алгебра
Популярные вопросы
- Язык. чтобы безударный гласный стал : морской-...
2 - Раскройте скобки, употребляя глаголы в present, past или future simple. i...
1 - Чем искусственные сообщества отличаются от природных...
2 - Мне. проведите консультация как отпределять валентность элементов . 1- по...
1 - Почему многие двукрылые считаются потенциально опасными для человека...
3 - Найдите все значения х, при которых значение дроби х^2+2х-3 делённое на х^2+5х-1...
1 - Сочинение по на тему путешествие по древнему египту...
2 - Музыкалная песнякакие песни ещё есть...
3 - Переведите 1 it took the auto-works in nizhny novgorod and moscow a very short...
1 - За четыре дня со склада вывезли 4060 тонн угля. в первый день вывезли 2/7...
1
Для решения данного уравнения, мы сделаем замену: t = x-5
Теперь у нас получается новое уравнение: t² - t + 2 = 0
Для решения этого квадратного уравнения, воспользуемся теоремой Виета, которая гласит, что сумма корней квадратного уравнения равна отрицательному линейному коэффициенту (в данном случае -1), а произведение корней равно свободному члену (в данном случае 2).
Сумма корней: t₁ + t₂ = 1
Произведение корней: t₁ × t₂ = 2
Теперь найдем значения t₁ и t₂. Разложим произведение 2 на два числа, сумма которых равна 1. Единственная комбинация это 2 и 1:
t₁ = 2
t₂ = 1
Теперь нам нужно записать ответ для t, а затем найти значения x.
t₁ = x - 5
t₂ = x - 5
Для t₁:
2 = x - 5
x = 2 + 5
x = 7
Для t₂:
1 = x - 5
x = 1 + 5
x = 6
Таким образом, уравнение имеет два возможных значения x: x = 7 или x = 6.