Вычислите значение 3tg a/2 , если sin a = -(24/25) pi<a<3pi/2

можно с решением
не могу понять данные задания ​

-4

Объяснение:

sin a = -(24/25) , cos²α=1-sin²α=1-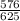=  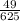,   cosα= - 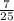, тк π<a<3π/2.

tg    ,/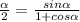

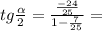
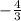3tg (a/2)=3* (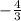 )=-4

вычислите значение 3tg α/2 , если sinα = -(24/25)   ,π <α <3π/2 .

ответ:  -4

Объяснение:    

tg(α/2)=sin(α/2)/cos(α/2) =2sin(α/2)*cos(α/2) /2cos²(α/2) =sinα/(1+cosα)

- - - - - - -

T.к.  0 <α <3π/2 , то cosα = -√(1 -sin²α)  = - √(1 -(24/25)²) =

- √((1 -24/25)(1+24/25) ) = --7/25 .

3tg (α/2) =3sinα/(1+cosα)  = 3*(-24/25) /(1- 7/25) = -72 / 18  = -4 .

* * * π <α <3π/2  ⇔π/2 <α <3π/4    ⇒tg (α/2) < 0 * * *