Вычислите: ответ запишите в виде несократимой дроби.
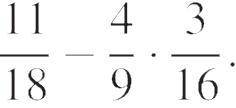
Другие вопросы по теме Алгебра
Популярные вопросы
- Скорость тела со свободно падающей массой 5000 г варьируется от 2 м /...
2 - Напишите дефиниции со словом embarrassed, полностью предложением....
2 - 29. 1) Что означает кратное натурального числа? Какое чис ДО называется...
2 - Посмотрите картинку вставьте пропущенные слова в текст пока melon опреснение...
1 - Надо на казахском составить предложение из этих слов жалық, қала, зейнеткер,...
2 - 1. Что такое географическая карта?...
3 - Волны с шумом набегали на берег-берег разбор по членам предложениям?...
3 - Выпешите все числа натурального ряда, расположенные между числами : 1...
1 - 6.Мақал-мәтелді толықтыр:Дос сыртыңнан ..., Дұшпан көзіңе ... . А)мақтар...
3 - Видно ли пластилы ? Если да, то когого они цвета...
1
Сначала найдем общий знаменатель для дробей 4/5 и 2/3. Общий знаменатель можно найти как произведение знаменателей каждой дроби:
5 * 3 = 15
Теперь приведем дробь 4/5 к общему знаменателю 15. Для этого умножим числитель и знаменатель на число, которое превратит знаменатель 5 в 15:
(4/5) * (3/3) = (12/15)
Аналогично, приведем дробь 2/3 к общему знаменателю 15:
(2/3) * (5/5) = (10/15)
Теперь мы можем сложить дроби (12/15) и (10/15):
(12/15) + (10/15) = (22/15)
Теперь сложим целую часть 2 и 3:
2 + 3 = 5
Итак, ответ будет:
5 22/15
Однако, нам нужно представить ответ в виде несократимой дроби. Для этого необходимо сократить полученную дробь 22/15. Общий делитель для чисел 22 и 15 равен 1, так как эти числа взаимно просты. Следовательно, дробь не может быть сокращена и ответ остается несократимым:
5 22/15