Вычислить по формуле ньютона-лейбница определенный интеграл.

Ответы

BOYKO10 24.05.2020 15:23

Ну для начала возьмем все таки этот интеграл (сначал можно как неопределенный)

$\int{\frac{e^\sqrt(x)}{\sqrt(x)}}\, dx=$ {сделаем замену $u=\sqrt{x}, du=\frac{1}{2\sqrt{x}}dx$ } продолжаем вычисление $=2\int{e^u}\, du=2e^u+C$

Теперь вернемся к исходным переменным: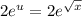 $2e^u=2e^{\sqrt{x}}$

Интеграл взяли, теперь вспоминаем формулу Ньютона-Лейбница: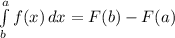 $\int\limits^a_b {f(x)} \, dx=F(b)-F(a)$ , где F(x)-какая-либо первообразная от функции f(x). Выше мы нашли первообразную от f(x) и она оказалась равна F 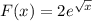$F(x)=2e^{\sqrt{x}}$ , константу здесь сделали 0.

Ну и теперь получаем

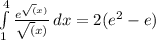
$\int\limits^4_1{\frac{e^\sqrt(x)}{\sqrt(x)}}\, dx=2(e^2-e)$

ответ: $\int\limits^4_1{\frac{e^\sqrt(x)}{\sqrt(x)}}\, dx=2(e^2-e)$

Примечание: почему я сначала брал неопределенный интеграл?

Потому что при любой замене в определенном интеграле необходимо пересчитывать пределы интегрирования.

Но поскольку мы пользуемся формулой Ньютона-Лебница в которой нам нужно найти именно первообразную, то можно воспользоваться и неопеределенным интегралом, чтобы ничего не пересчитывать.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра