1. Алгебра
  2. Вычислить интеграл по частям

Вычислить интеграл по частям 1 Пример нужна пример по теме ;
Интегралы по частям!
За правильный ответ накину балов! и оценку и все что угодно!


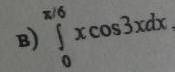
Вычислить интеграл по частям 1 Пример нужна пример по теме ; Интегралы по частям! За правильный отв

armeninkrasavcheg armeninkrasavcheg    2   04.12.2020 17:44    0

Ответы
annelya009 annelya009  04.12.2020 17:50

∫x•cos3xdx

Объяснение:

∫x•cos3xdx=

u=x => du=dx

dv=cos3xdx => v=⅓sin3x

=(x/3)•sin3x-⅓∫sin3xdx=(x/3)•sin3x+⅟₉•cos3x+C

или: (X^2)/2-(sin3x)/3

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
vovamandrik060p09ui1 vovamandrik060p09ui1  13.04.2020 18:27
Сума четвертого і одинадцятого елементів арифметичної прогресії дорівнює 36 а сьомий елемент цієї прогресії дорівнює 20.Знайдіть різницю прогресії. З рішенням...
Smolensk145 Smolensk145  13.04.2020 18:27
У используя формулы сокращенного умножения: (p+3)^2+(3p-1)(3p+1)...
tln72 tln72  13.04.2020 18:26
Х = 2, xy = 2. Знайдіть q i x6​...
amozgaleva96 amozgaleva96  13.04.2020 18:26
Какие из точек А(0; 7), B(4; -1), C(1; 10), D(-2; –3)принадлежат графику уравнения -3y + х = 7?​...
тая112 тая112  13.04.2020 18:26
Дана функция ()=82+1−10. Вычисли (0)= . ответить!...
777SwimmeR777 777SwimmeR777  13.04.2020 18:26
Разложи на множители (x+7y)2−(7x+y)2. Выбери правильный ответ: −48x2+48y2 другой ответ 48(x2−y2) (−6x+6y)⋅(8x+8y) (x2+49y2)⋅(49x2+y2) (x2+14xy+49y2)−(49x2+14xy+y2)...
rzd1 rzd1  13.04.2020 18:26
При якому значенні аргументу функції y=5x + 10 дорівнює -5?...
kirill12123 kirill12123  13.04.2020 18:26
Якласс, 8 класс. Алгебра. Задания на скринах. Срок до завтра....
polina19a polina19a  13.04.2020 18:26
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме сторона каждой клетки на плане равна 0,5 м вход в квартиру находится в прихожей напротив входа располагается...
Вика1774574747 Вика1774574747  13.04.2020 18:26
При каких значениях переменной x имеет смысл выражение корень (x-5)(x+6)...

Популярные вопросы