во Составьте какое-нибудь уравнение с двумя переменными и найдите три его решения
2. Какие из пар чисел (4; -5) (-2; 5) (1; 2,5) (6; -15) являются решением уравнения x²+2y - 6 = 0
Другие вопросы по теме Алгебра
Популярные вопросы
- Каким разделить смесь крупы и соли; смесь песка и опилок; смесь песка со...
3 - Используя числа : а ) 20, 4 и 80; б)200, 4 и 800,составь четыре верных числовых...
1 - Отметить на плоскости четыре точки так, чтобы ни какие три не лежали на одной...
3 - Как правильно разобрать слово тренировка по составу.однокоренные слова слова...
1 - Впрямоугольнике точка пересечения диагоналей удалена от большей стороны на...
2 - Что сказка царевна лягушка волшебная, о животных ,бытовая?...
3 - Машина равеомерно двигалась со скоростью 36 км/ч в течени 20 секунд .какой...
1 - Каток массой 6 т имеет площадь. 200с в кводрате . какое давление он окащывает...
1 - Pb (no2)3+na2so4 составление ионных уравнений...
1 - Какую работу может завершить за 10 минут двигатель мощность которого 10 квт...
3
1.
Пусть х=0:
Пусть у=0:
Пусть х=1:
Три решения: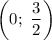 ,
, 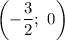 ,
, 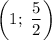
2.
Проверим, выполняется ли равенство после подстановки соответствующих координат в уравнение: