В уравнении 3x во второй степени -5х+k=0, один из его корней равен -3 найди другой корень и свободный член k
Другие вопросы по теме Алгебра
Популярные вопросы
- Длина прямоугольника 65 см, ширина 1 дм 7 см. найди периметр и...
2 - Дайте краткое содержание ревизора по действиям: 3 заранее : )...
3 - Определить род ,число и падеж прилагательных в неярком свете взором...
1 - Нужно найти глаголы. замени, где возможно, глаголы несовершенного...
1 - Сочинение на тему моя любимая буква...
1 - Великие люди с профессией ветеринара...
3 - Вес тела равен силе тяжести, если тело движется а) прямолинейно...
3 - Составить рассказ на тему моя любимая игрушка...
3 - Эту нам дали из электива по информатики начинаться должно так...
1 - Автор трагедий в стихах фауст? а) гейне б) гёте в) байрон г) гюго...
2
Объяснение:
вспоминаем, как определяются корни квадратных уравнений:
1. по теореме Виета: х₁+х₂=-в/a х₁*х₂=к/a подставляем в формулы
-3+х₂= 5/3 х₂=5/3+3=14/3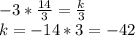
2. через дискриминант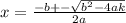 проверка решения:
проверка решения: