Упростите выражение : cos ²2 x+(1+cos2x)²tg²x
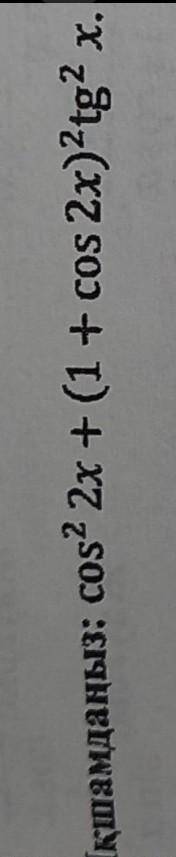
Другие вопросы по теме Алгебра
Популярные вопросы
- Нужно найти значение выражения - 3\4 x^2 (x+3) = ? при x = 1 1\3...
1 - Вычислить силу действующую на бочку с медом массой 300 кг чему равна...
2 - Скажите таблица распределения кратностей имеет вид: вариант 0 1 3 5...
3 - Переделать тест в косвенную речь* the most famous one is probably tower...
2 - Кітапханашыдан сұхбат алып диалог құру...
1 - Создайте программу на паскале. программа вводит случайный массив из...
1 - В. напиши, какие памятники и культуры есть в вашем селе(городе).в городе...
3 - Мектеп кітапханасы кітапхана туралы кітапханашыдан сұхбат алып диалог...
3 - Вычислите площадь фигуры, ограниченной линиями y=x^3, y=x^2, x=-2,...
3 - Рассказ на тему «что я понял, рассмотрев картину м. шагала день рождения»...
1
1. Тождество синуса: sin²x + cos²x = 1
2. Тождество косинуса: cos²x = 1 - sin²x
3. Тождество тангенса: tg²x = sin²x / cos²x
Используя эти тождества, приступим к упрощению выражения пошагово:
cos ²2 x + (1 + cos2x)²tg²x
1. Заменим cos²x с помощью тождества косинуса:
(1 - sin²2x) + (1 + cos2x)²tg²x
2. Возведем (1 + cos2x) в квадрат:
(1 - sin²2x) + (1 + 2cos2x + cos²2x)tg²x
3. Упростим tg²x с помощью тождества тангенса:
(1 - sin²2x) + (1 + 2cos2x + cos²2x)(sin²x / cos²x)
4. Упростим дробь (sin²x / cos²x) на основании тождества синуса:
(1 - sin²2x) + (1 + 2cos2x + cos²2x)(sin²x / (1 - sin²x))
5. Упростим выражение под знаком умножения:
(1 - sin²2x) + (sin²x + 2cos2xsin²x + cos²2xsin²x) / (1 - sin²x)
6. Умножим sin²x на (1 - sin²2x) и sin²x на (cos²2x + 2cos2x):
(1 - sin²2x) + (sin²x - sin⁴2x + 2cos2xsin²x + cos²2xsin²x) / (1 - sin²x)
7. Сгруппируем слагаемые синуса и косинуса:
1 + sin²x - sin⁴2x + 2cos²xsin²x + cos²2xsin²x - sin²2x
8. Упростим слагаемые:
1 + sin²x - sin⁴2x + (cos²x + sin²x)sin²2x - sin²2x
9. Упростим сумму sin²x и cos²x с помощью тождества синуса:
1 + sin²x - sin⁴2x + sin²2xsin²x - sin²2x
10. Упростим суммы и разности слагаемых:
1 - sin⁴2x + sin²x(sin²2x + 1 - 1) - sin⁴2x
11. Найдем значение sin²2x + 1 с помощью тождества синуса:
1 - sin⁴2x + sin²x * 2cos²x - sin⁴2x
12. Упростим:
1 - sin⁴2x + 2sin²x * cos²x - sin⁴2x
13. Распишем cos²x как 1 - sin²x:
1 - sin⁴2x + 2sin²x * (1 - sin²x) - sin⁴2x
14. Упростим:
1 - sin⁴2x + 2sin²x - 2sin⁴x - sin⁴2x
15. Сгруппируем слагаемые:
1 - 2sin⁴x - 2sin⁴2x + 2sin²x
16. Избавимся от минусов в начале выражения:
1 + 2sin⁴x + 2sin⁴2x - 2sin²x
Таким образом, упрощенное выражение равно 1 + 2sin⁴x + 2sin⁴2x - 2sin²x.