Упростить выражение не могу справится
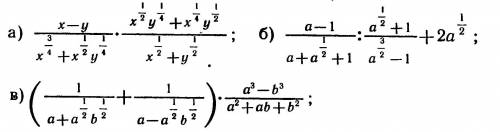
Другие вопросы по теме Алгебра
Популярные вопросы
- Определи подтверждающие факты к предложенному аргументу Аргумент: Изучение...
2 - Таблица N 1, ЖилищеКухняназваниеиз чего сделаноинтерьердворпосудаЗадание по...
1 - Извини, что достала, но мне опять нужна!...
2 - 8. Музей мировой погребальной культуры города Новосибирска хранит предмет,...
2 - Назовите особый вид монологической речи a. исповедь b. рассуждение c. внутренний...
2 - Определи верные и неверные утверждения о горючих полезных ископаемых. Сведения:...
3 - 4.На расстояние 6 см напряженность электрического поля 20 кВ\м, а величина...
3 - 1)Назовите персонажей рассказа Чехова «Дипломат» 2)Почему так назван рассказ?3)С...
2 - А выделеные-в тексте слова-это?А)синонимы Б)омонимыС)АнтонимыД)Фразеологизм...
2 - . Сравните нервные системы: Диффузная Лестничная Узловая Трубчатая животное...
2
1. Для начала обратим внимание на знаки операций. Мы видим, что между слагаемыми стоит знак минус. Помним, что при умножении знаков одного типа (положительного или отрицательного) результат будет положительным, а при умножении знаков разных типов - отрицательным.
2. Рассмотрим числитель и знаменатель отдельно. У нас имеется два слагаемых в числителе и два в знаменателе. Мы можем произвести умножение внутри скобок.
3. Начнем с числителя: (3x - 6) * (5 - 2x). Для умножения двух скобок будем использовать правило распределительного свойства. Умножим каждое слагаемое из первой скобки на каждое слагаемое из второй скобки и сложим полученные произведения:
(3x - 6) * (5 - 2x) = 3x * 5 + 3x * (-2x) - 6 * 5 - 6 * (-2x)
4. Сократим каждое слагаемое:
= 15x - 6x^2 - 30 + 12x
5. Соберем все слагаемые вместе:
= -6x^2 + 27x - 30
6. Теперь рассмотрим знаменатель: (-4 - x) * (3 - 2x). Проведем аналогичные действия и выполним распределение:
(-4 - x) * (3 - 2x) = (-4) * 3 + (-4) * (-2x) + (-x) * 3 + (-x) * (-2x)
7. Сократим каждое слагаемое:
= -12 + 8x - 3x - 2x^2
8. Соберем все слагаемые вместе:
= -2x^2 + 5x - 12
Таким образом, упрощенное выражение будет:
(-6x^2 + 27x - 30) / (-2x^2 + 5x - 12)
Обратите внимание, что эти два многочлена необходимо обозначать в скобках, чтобы избежать недоразумений при чтении.