1. Алгебра
  2. Упростить выражение: √18 (√6-√2)

Упростить выражение: √18 (√6-√2) -3√12

Dimka14228 Dimka14228    1   24.06.2020 19:35    2

Ответы
sab1na666 sab1na666  15.10.2020 14:49

\sqrt{18}\cdot (\sqrt{6}-\sqrt{2})-3\sqrt{12}=\sqrt{18}\cdot \sqrt6-\sqrt{18}\cdot 2-3\sqrt{3\cdot 4}=\\\\=\sqrt{3\cdot 6}\cdot \sqrt6-\sqrt{9\cdot 2}\cdot \sqrt{2}-3\cdot 2\sqrt3=\sqrt{3\cdot 6^2} -\sqrt{9\cdot 2^2}-6\sqrt3=\\\\=6\sqrt3-3\cdot 2-6\sqrt3=-6

ПОКАЗАТЬ ОТВЕТЫ
nastyagrigorov nastyagrigorov  15.10.2020 14:49

-6

Объяснение:

\sqrt{18} *(\sqrt{6} -\sqrt{2} )-3\sqrt{12}

Выделим полный квадрат: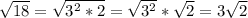 \sqrt{18} =\sqrt{3^2*2} =\sqrt{3^2} *\sqrt{2} =3\sqrt{2}

Выделим полный квадрат и упростим: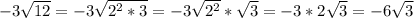 -3\sqrt{12} =-3\sqrt{2^2*3} =-3\sqrt{2^2} *\sqrt{3} =-3*2\sqrt{3} =-6\sqrt{3}

Теперь выражение имеет вид: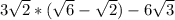 3\sqrt{2} *(\sqrt{6} -\sqrt{2} )-6\sqrt{3}

Умножим число на скобки: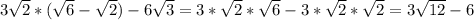 3\sqrt{2} *(\sqrt{6} -\sqrt{2} )-6\sqrt{3}= 3*\sqrt{2} *\sqrt{6} -3*\sqrt{2}*\sqrt{2}=3\sqrt{12} -6

Получаем: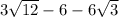 3\sqrt{12} -6-6\sqrt{3}

Выделяем полный квадрат: 3\sqrt{12} =3\sqrt{2^2*3} =3*\sqrt{2^2} *\sqrt{3} =6*\sqrt{3}

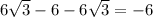В итоге: 6\sqrt{3} -6-6\sqrt{3}=-6 (сократили)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
EkimovaVlada EkimovaVlada  01.09.2019 16:50
найдите наименьшее целое число, удовлетворяющее неравенству: (x-9)² - (x+3)(x+5) ≤ 6...
gels5344Inetka gels5344Inetka  20.05.2019 16:40
Смешав 40 процентный и 45 процентный растворы кислоты и добавив 10 кг чистой воды, получили 39 процентный раствор кислоты. если бы вместо 10 кг воды добавили 10 кг 50 процентного...
luiza151661 luiza151661  20.05.2019 16:40
Решите уравнение: а) 3x-2√x-8x=0 б) √2x+15=x...
31101960 31101960  20.05.2019 16:40
Докажите , что функция y=4: x-2 убывает при x 2...
nikolaivanov11 nikolaivanov11  20.05.2019 16:40
Известно , что в прогрессии (bn): b2=4; b3=12.ответьте на вопросы: 1)чему равен знаменатель прогрессии q ? q= 2) чему равен первый член прогрессии? b1= 3) какова формула n-ого члена...
Strelok09245 Strelok09245  20.05.2019 16:40
Дана арифметическая прогрессия 6.8. сумму первых 60-ти ее членов...
GordienkoA20 GordienkoA20  20.05.2019 16:40
При каких значениях переменной х значения двучлена 0,5-0,2х принадлежит промежутку [ -1/2; 1/2]...
vagiz7000 vagiz7000  20.05.2019 16:40
Решить систему уравнений 3x^2+xy=35 2x-y=30...
vadimgricuk74 vadimgricuk74  20.07.2019 05:00
В△mnk угол m тупой. тогда другие два...
snysor snysor  20.07.2019 05:00
Вычислить: √1целая11/25-√0,04+√6²+8²...

Популярные вопросы