Точками пересечения функции y = sin(x) и y = 0,5 на отрезке [0,3] являются точки:

Ответы

знания436 19.07.2022 20:47

Решение.

Точки пересечения функций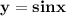 $\bf y=sinx$ и y=0,5 находим , решив

уравнение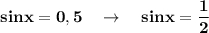 $\bf sinx=0,5\ \ \ \to \ \ \ sinx=\dfrac{1}{2}$ .

$\boldsymbol{\bf x=\dfrac{\pi }{6}+\pi n}$ или $\boldsymbol{\bf x=\dfrac{5\pi}{6}+\pi n}\ \ ,\ \ \bf n\in Z$

Мера заданного отрезка [ 0 , 3 ] выражена в радианах ,

$\bf 3\ rad\approx 171,9^\circ\ \ ,\ \ \dfrac{\pi}{6}=30^\circ \ \ ,\ \ \dfrac{5\pi }{6}=150^\circ$

Поэтому точки пересечения заданных графиков, принадлежащих указанному промежутку - это точки

$\boldsymbol{\bf \Big(\, \dfrac{\pi}{6}\ ;\ \dfrac{1}{2}\ \Big)\ \ ,\ \ \ \Big(\ \dfrac{5\pi }{6}\ ;\ \dfrac{1}{2}\ \Big)}$

ответ: №4 .

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

kirapri32 09.11.2020 16:47

5polinka 09.11.2020 16:48

Задание а) вычислите От 7 до 30...

kamilla202 09.11.2020 16:48

geniynayk 14.02.2021 22:20

ersultanplay 14.02.2021 22:22

Найдите значение выражения 1,6-2,8•0,2...

Kevand 14.02.2021 22:26

Алгебра 7 класс Решите то что на фото...

jovanny1607 14.02.2021 22:27

супер567890 14.02.2021 22:28

лера2285 14.02.2021 22:29

aibekauezhanme 01.09.2019 02:10