Точка K рухається по прямій 6x-8y-17=0 Якою буде мінімальна відстань від точки K до нерухомої точки P (3;-5)?
d=
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите значение выражения (5 + √2)² + (5 - √2)² прям...
1 - Выражение 7/12(6а+24)-2/4(18 в-9) и найдите его значение при а 7 1/3 в...
3 - Проанализируйте образ марии мироновой и представьте свою работу в виде...
2 - Запустить вы снова правы закономирности поширення паливно енергетичних...
3 - Основы трапеции равны 4 см и 12 см . а боковые стороны 5 см и 6 см. на...
1 - 100 .на странице 20 строк по 60 символов.на хранение одного символа требуется...
3 - Астронавтың ай бетіндегі салмағы жер бетіндегімен салыстырғанда өзгере...
1 - Рисунок на тему изобретение будущего. идеи...
2 - Чем по питания авторотрофы отличается от гетеротровов...
2 - Решить тест по органической . в залог 55 ; заранее огромное )...
2
Мінімальна відстань від точки до прямої — це перпендикуляр, тому K має бути основою перпендикуляра від точки K на пряму 6x-8y-17=0.
Знайдемо кутовий коефіцієнт (далі — КК) заданої прямої:
КК перпендикулярних прямих пов'язані співвідношенням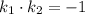 , тому КК перпендикуляра дорівнює:
, тому КК перпендикуляра дорівнює:
Рівняння прямої з КК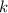 , яка проходить через точку
, яка проходить через точку 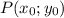 , має вигляд:
, має вигляд:
Щоб знайти координати точки K, складемо систему з рівнянь двох прямих:
Итак, координаты точки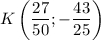 . Найдём |PK|:
. Найдём |PK|:
Відповідь: 4,1 од.