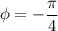найти корни из компл.чисел
найти корни из компл.чисел
Другие вопросы по теме Алгебра
Популярные вопросы
- Сувеличением или уменьшением энтропии протекает процесс разложения карбоната кальция?...
3 - Какое количество тепла потребуется для разложения 5,0 г карбонита кальция по реакции...
3 - Задайте 4 типа вопроса к предложению: mike and i are in the yard....
2 - Определите массу борной кислоты , которая получится при взаимодействии 6.8 г бора...
2 - 1) изобразите схематически график функции а) у=3х^2, б)у=-2(х+1)^2 2)постройте...
1 - Что в результате ch3clmg + h2o -- ?...
2 - Вычислить дельтан298 пропана, если известно, что при сжигании 11г пропана в кислороде...
1 - Тело массой 400 г, двигаясь прямолинейно с некоторой начальной скоростью, за 5...
2 - При измерении напряжения в сети переменного тока показания вольтметра составили...
2 - 8х в кубе+12х в квадрате у+6ху в квадрате+у в кубе= решите кто нить плз...
1
Рассмотрим комплексное число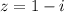 , его модуль
, его модуль 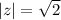 . Тогда
. Тогда
Поскольку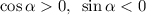 то
то