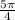-4=0) на отрезке [pi ; 5pi/2]
на отрезке [pi ; 5pi/2]
Другие вопросы по теме Алгебра
Популярные вопросы
- Написать статью о таинственном месте в Таразе которая привлекает людей 200-300...
2 - 4. Напишите рекламный текст для учащихся об открытии «Школы иностранных языков»....
2 - Где можно встретить необычные скульптуры Роя Лихтенштейна? в Бразилиив Южной...
2 - Сделать схемы сложных предложений определить вид придаточных в сложноподчиненных...
2 - Сделайте вывод о положении Казахского ханства во время их правления...
1 - 600×(8,671-2,271)×2,05+7,68=7879,68...
1 - 10 КЛАСС С КОНТРОЛЬНОЙ ПО МАТЕМАТИКЕ. от с заданием, очень нужноЗадание:(√3)4;...
3 - Расст...лать скатерть разб...ру вещипроб...рался сквозь заросливыд... paть...
1 - Освободитесь от иррациональности в знаменателе дроби: 5 задание...
3 - 4.Төмендегі сұраққа бір сөйлеммен жауап беріңіз. Мәтінде климат өзгеруінің...
1
Объяснение:
2sin²x - 3√2cosx - 4 = 0
2(1 - cos²x ) - 3√2cosx - 4 = 0
2 - 2cos²x - 3√2cosx - 4 = 0
-2cos²x - 3√2cosx - 2 = 0
2cos²x + 3√2cosx + 2 = 0
Замена: cosx = t, t ∈ [-1 ; 1]
2t² + 3√2t + 2 = 0
D = 18 - 16 = 2
t₁ =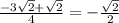
t₂ =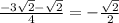 ∉ [-1 ; 1]
∉ [-1 ; 1]
cosx =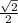
x = ±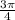
На отрезке
x =