 \leqslant - \frac{ \sqrt{3} }{2} ) 30 решить тригонометрическое неравенство
30 решить тригонометрическое неравенство
Ответы

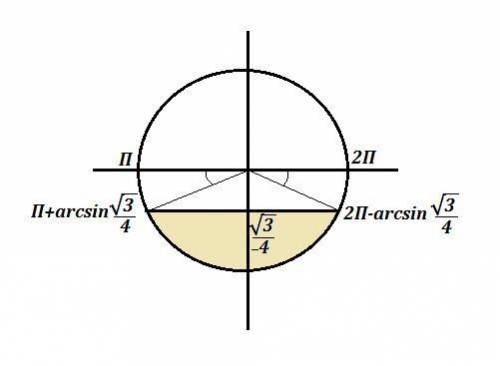 30 решить тригонометрическое неравенство" />
30 решить тригонометрическое неравенство" />
Другие вопросы по теме Алгебра
Популярные вопросы
- история 6 класс Как звали крестьян которые взяли что либо у...
1 - Отметьте на контурной карте направления маршрутов путешественников:...
1 - Exercise 17. Translate the sentences using the Present Participle....
2 - Якщо напрям прискорення співпадає з напрямом руху тіла,то модуль...
2 - Длинна триугольного паралелепипеда ровняется 12 см, шырина —...
3 - 4) На рисунке дан план огорода прямоугольной формы в масштабе...
1 - 1) Порівняти образи Дон Кіхота і Санчо Панси(4 речення) 2) Що...
1 - Задача: Коло діаметром якого є відрізок АС, описане навколо...
1 - Хорда AB образует с диаметром окружности угол величиной 40°....
3 - Зробіть розбір виділеного слова як частини мови ЗБИРАЮЧИ перлини...
3