1)найдите сумму первых двенадцати членов арифметической прогрессии (an) , если :
a) а1=3 , d=2;
б) а1= –1 , d= 4;
в) а1 = 5 , d = –3
г) а1= 6 , d = 1
2) найдите сумму всех натуральных чисел :
а) от 1 до 200 б) от 1 до 300 в) от 10 до 150

Ответы

zhuniorneimar486 12.10.2020 02:50

Задание 1

Сумма арифметической прогрессии считается по формуле:

$S_n = \frac{2a_1+d(n-1)}{2} \cdot n$

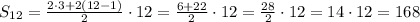
а) $S_{12} = \frac{2\cdot3 + 2(12-1)}{2} \cdot12 = \frac{6+22}{2} \cdot12 = \frac{28}{2} \cdot 12 = 14\cdot 12 = 168$

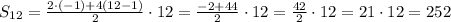
б) $S_{12} = \frac{2\cdot(-1) + 4(12-1)}{2} \cdot12 = \frac{-2+44}{2} \cdot12 = \frac{42}{2} \cdot 12 = 21\cdot 12 = 252$

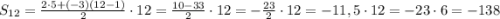
в) $S_{12} = \frac{2\cdot5 + (-3)(12-1)}{2} \cdot12 = \frac{10-33}{2} \cdot12 = -\frac{23}{2} \cdot 12 = -11,5 \cdot 12 = -23 \cdot 6 = -138$

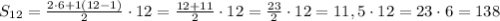
г) $S_{12} = \frac{2\cdot6 + 1(12-1)}{2} \cdot12 = \frac{12+11}{2} \cdot12 = \frac{23}{2} \cdot 12 = 11,5\cdot 12 = 23 \cdot 6 = 138$

Задание 2

а)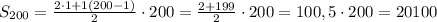 $S_{200} = \frac{2\cdot 1 + 1(200-1)}{2}\cdot 200 = \frac{2 + 199}{2} \cdot 200 = 100,5 \cdot 200 = 20100$

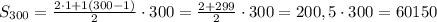
б) $S_{300} = \frac{2\cdot 1 + 1(300-1)}{2} \cdot 300 = \frac{2+299}{2} \cdot 300 = 200,5\cdot 300 = 60150$

в) $S_{150} = \frac{2\cdot 10 + 1(150 - 1)}{2} \cdot 150 = \frac{20+149}{2} \cdot150 = 84,5 \cdot 150 = 12675$

Удачи!

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

dree123 05.11.2020 15:04

Любимая0105 03.05.2020 14:07

yuliyabondar2 03.05.2020 14:07

elizavetadeomi 03.05.2020 14:07

решить линейное уравнение{ 1-3х/4 -4-2у/3=0 { 0,7=0,4у-0,3х...

Danil111112 21.11.2021 01:56

умница2423 21.11.2021 01:58

jurakos9 21.11.2021 01:58

академег228 21.11.2021 01:59

РЕШИТЕ 4 ЗАДАНИЕ ОБА ПРИМЕРА...

maksgibert61 21.11.2021 02:04

F(x)=x2+5 знайдіть f(0) f(-4)...

katy54445 21.11.2021 02:05

Найдите координаты вершины параболы y=-x2+2x...