Сумма 50 натуральных чисел равна 2950 . Все эти числа разбили на три группы. Известно, что:
- в первой группе 43 чисел, их среднее арифметическое равно 18
- среднее арифметическое чисел второй группы равно 59
- среднее арифметическое чисел третьей группы - целое число.
Найдите количество чисел в третьей группе
надо(
Другие вопросы по теме Алгебра
Популярные вопросы
- Есть ли тут ошибка? У насекомых и ракообразных глаза фасеточные,...
3 - Установіть відповідність між організмом і типом організації 1 одноклітинні...
2 - Какой процесс — окисление или восстановление — отражает схема: C−4−4e−→C0...
3 - Решите с пояснениями Точка движется по кривой так, что её координаты...
3 - Найти:625 : х =5 236: х =59 х...
3 - Яка маса міді виділиться на електроді під час електролізу мідного...
1 - Антуан де Сент-Экзюпери маленький принц чистота восприятия мира...
3 - с сольфеджио класс Построить аккордовую последовательность в тональности...
3 - В деревне у мамы два трудолюбивых ребёнка: Аня и Юра. Аня может...
2 - Дописать уравнения возможных реакций: А) Mg + Pb(NO3)2 → Б) Zn +...
1
Найдем сумму чисел в первой группе:
Найдем сумму чисел во второй и третьей группе:
Заметим, что во второй и третьей группе вместе чисел было:
Введем обозначения. Пусть во второй группе было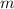 чисел, а в третьей группе было
чисел, а в третьей группе было 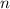 чисел. Среднее арифметическое чисел второй группы по условие равно 59, а среднее арифметическое чисел третьей группы обозначим как
чисел. Среднее арифметическое чисел второй группы по условие равно 59, а среднее арифметическое чисел третьей группы обозначим как 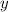 .
.
В этих обозначениях нам нужно найти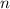 .
.
Можем записать два равенства:
Из первого равенства выразим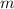 :
:
Подставим во второе равенство:
Так как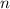 - количество чисел, то это число должно быть целым (как минимум, неотрицательным). Также, по с условию
- количество чисел, то это число должно быть целым (как минимум, неотрицательным). Также, по с условию 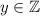 . Значит, число
. Значит, число 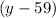 является делителем числа
является делителем числа  . Тогда есть 4 варианта:
. Тогда есть 4 варианта:
Однако, не все эти 4 варианта реализуемы. Вспомним, что количество чисел третьей группы связано с количеством чисел второй группы соотношением:
Так как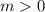 , то:
, то:
Такому условию удовлетворяет только вариант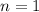 .
.
ответ: 1