1. Алгебра
  2. Сколько различных пятизначных

Сколько различных пятизначных чисел без повторения цифр можно составить из цифр 1,2,5,7,8

матиматик31 матиматик31    3   27.06.2019 02:50    6

Ответы
BettaPi2003 BettaPi2003  21.07.2020 17:58
Решение:    

Рассуждать при решении задачи нужно так:

На первое место в наше число мы можем поставить любую из \textsl {5} имеющихся цифр (\textsl {1, 2, 5, 7, 8}). То есть, у нас \textsl{5} и никакой из них не ограничивается законом.Со вторым местом небольшая проблема: мы не можем любую из \textsl{5} цифр туда поставить, так как одна из них уже была использована. Значит, мы можем поставить на почетное второе место любую из \textsl{4} оставшихся цифр.Для третьего места есть ровно \textsl{5 - 2 = 3} так как 2 цифры из \textsl{5} уже использовались).Не потеряем нить рассуждения и заметим, что для четвертого места ровно \textsl{2} а для пятого, последнего, - не иначе, как одно.Итого мы будем иметь \textsl {5 * 4 * 3 * 2 * 1 = 120}

А можно, без всяких лирических отступлений, сказать, что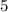 5 чисел мы можем выставить в ряд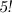 \textsl{5!}

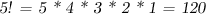\textsl{5! = 5 * 4 * 3 * 2 * 1 = 120}.

При этом формула для \textsl{n!} ("эн факториал") такая: \textsl{n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1}.

Задачу уже мы решили!

ответ:  \thefontsize\Large \boxed{\bold{\texrsl{120}}} .
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
sfdfgdfgdfg sfdfgdfgdfg  12.09.2021 21:02
Не только ответ, с объяснением...
PomidorkaX3 PomidorkaX3  12.09.2021 20:59
Вычисли ctg t, если t равно −7π/3....
ressoli444 ressoli444  12.09.2021 20:59
Виноград содержит 95% влаги, а изюм 6%. Сколько килограммов винограда потребуется для получения 50 кг изюма?...
клубничка188 клубничка188  12.09.2021 20:57
В равнобедренном треугольнике АВС (АВ=ВС) проведены биссектрисы АN и СК. а) Докажите, что отрезок КN параллелен стороне АС б) Докажите, справедливость равенств АК=КN=NC...
KÆTÉ KÆTÉ  12.09.2021 20:57
Будувати графік і вказати проміжки монотонності y= (x-1)²-3...
leda5 leda5  12.09.2021 20:56
Найти первообразнуюf ( x ) =3/sin²x-9x⁸ ....
рух123 рух123  12.09.2021 20:54
(х-3)²-(х-4)=10 (2у+1)²-4у-2)=5-у...
ROMA2K18 ROMA2K18  12.09.2021 20:51
Потрібно довести тотожність 2(3a+4b)+3(a-7-b)-7(2a-7b)= -5a + 36b...
Olyakiti Olyakiti  12.09.2021 20:50
1.Сформулируйте основное свойство расположения точек от носительно прямой на плоскости...
Elnura85 Elnura85  08.10.2019 00:20
1.решите уравнение: a.√2cosx = 1; b.sinx+cosx = 0; c.2cos2x-sinx = -1; d.(cos3x-1)sinx = 0. 2.решите неравенство: ctg(π/2+x) √3....

Популярные вопросы