Вычисли ctg t, если t равно −7π/3.
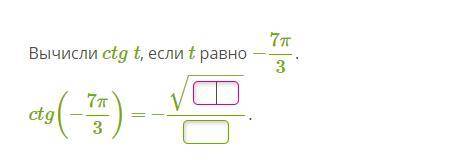
Другие вопросы по теме Алгебра
Популярные вопросы
- 1.3. Match the synonyms. create be concerned with branch equipment deal with develop...
3 - Условные предложения If she were underweight, she ___( eat) more carbohydrates....
2 - Почему у Бауыржана Момышулы нет фамилии?...
1 - 2. Умовний рефлекс виробляється на: * а) больовий подразник; б) будь-який подразник;...
3 - Сохраняя закономерность нарисуй в пустых клетках таблицы пропущенные монеты...
3 - Составить пищевую цепь реки Днепр ...
3 - Доведіть що 2 висоти трикутника не можуть точкою перетину ділитися навпіл Очень...
1 - XIX ғасырда өмір сүрген күйшілер...
1 - Дополни предложение и реши задачу...
3 - Найдите сторону ромба диагонали которого равны 24 и 70 дм Отправьте условие и решение...
3
2,1/1,7 это же легко...
Начнем с вычисления тангенса t.
Тангенс t определяется как отношение противоположной стороны к прилежащей стороне прямоугольного треугольника с углом t.
Из заданного значения t = -7π/3, мы видим, что угол t находится в третьем квадранте, где тангенс является отрицательным.
Теперь, чтобы найти противоположную и прилежащую стороны треугольника, мы можем использовать периодичность синуса, косинуса и тангенса в радианах.
Сначала найдем изначальный угол, который находится в первом квадранте и имеет то же значение тангенса.
Из формулы периодичности угла, мы можем добавить или вычесть период 2π, чтобы получить значения тангенса для углов, лежащих в первом квадранте.
-7π/3 + 2π = -7π/3 + 6π/3 = -π/3
Теперь, чтобы найти противоположную и прилежащую стороны в треугольнике с углом -π/3, мы можем использовать встроенные значения синуса и косинуса для этого угла.
sin(-π/3) = -√3/2
cos(-π/3) = 1/2
Используя эти значения, мы можем найти тангенс угла -π/3.
tan(-π/3) = sin(-π/3) / cos(-π/3) = (-√3/2) / (1/2) = -√3
Теперь, чтобы получить котангенс, мы можем использовать обратное значение тангенса.
cot(-π/3) = 1 / tan(-π/3) = 1 / (-√3) = -1/√3
Таким образом, ctg t, где t равно −7π/3, равно -1/√3.