Sin(4x)-3cos(4x)=8sin^2(2x) Решите буду благодарен)
Другие вопросы по теме Алгебра
Популярные вопросы
- Свойства перпендикуляра и наклонной 10класс...
1 - Вместо звездочек поставьте цифры так чтобы действие 10-4567*=55555...
3 - Поезд за 2 суток преодолел расстояние 9600 км. найти среднюю скорость...
3 - Если 900000 изделий на одной фабрике изготовили за 3 часа а другой за...
2 - Свойства перпендикуляра и наклонной 10класс...
3 - На березе сидят 10 воробьев, а на рябине на 6 больше. несколько воробьев...
2 - Напишите это хотя бы по ,если вы хорошо знаете анг. то по . про книку...
1 - Определите род имен существительных. аэрозоль, бандероль, канифоль, пемоксоль,...
2 - Решить уравнение x×100-594=2406 (со схемой)...
3 - Делитель увеличили в 6 раз. как надо изменить делимое чтобы частное уменьньшилось...
1
(см. объяснение)
Объяснение:
Т.к.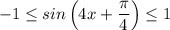 , то равенство всегда ложно.
, то равенство всегда ложно.
Поэтому уравнение не имеет корней.
Уравнение решено!