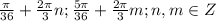Sin(3x+pi/4)=1/2. Решить уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Берілген сөздердің лексикалық мағынасын анықтап жазындар:қағида,құрылтай,тәжірибе...
3 - 8. Виберіть ознаки класу плазунів: а) шкіра тонка, має залози; б) череп...
2 - Гималай тауының биік нүктес...
3 - Task 1 Choose the correct words. She/He/lt a bicycle.1 lt/You/He are from...
2 - Изобразите множество точек, заданных системой неравенств:{х2+у2≤64 х+у≥5 ...
1 - Повість на тему Захар беркут і сучасна Україна(можна не з інтернету скопіювати...
1 - Заполнить таблицу « Особенности строения и образа жизни плоских, круглых...
2 - 2608 км/ч = м/мин. Результат округли до единиц.58 км/ч = см/с. Результат...
2 - составить небольшую статью на 150-200 слов)...
2 - 1)Факты, свидетельствующие о разложении феодальной системы хозяйства....
1
Замена переменной:
Уравнение:
Решаем по формулам:
Обратный переход :
k=2n
k=2n+1
О т в е т.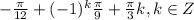 или
или