с алгеброй. Решите 2 примера с метода введения новой переменной или метода замены переменной ​

4. x = 1 ; 2 ; 3 ; 4

5. x =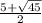   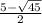; ; 3 ; 2

Объяснение:

4. (x² - 5x)(x² - 5x + 10) + 24 = 0

Произведем замену: (x² - 5x) = t

Тогда: t(t + 10) + 24 = 0

t² + 10t + 24 = 0

D = 10² - 4·24 = 100 - 96 = 4

;

Произведем обратную размену: t = (x² - 5x)

• (x² - 5x) = -4

x² - 5x + 4 = 0

D = (-5)² - 4·4 = 25 - 16 = 9

;

• (x² - 5x) = -6

x² - 5x + 6 = 0

D = (-5)² - 4·6 = 25 - 24 = 1

;

ответ: x = 1 ; 2 ; 3 ; 4

5. (x² - 5x + 2)(x² - 5x - 1) = 28

Произведем замену: x² - 5x = t

(t + 2)(t - 1) = 28

t² - t + 2t - 2 = 28

t² + t - 30 = 0

D = 1² - 4·(-30) = 1 + 120 = 121

;

Произведем обратную размену: t = (x² - 5x)

• x² - 5x = 5

x² - 5x - 5 = 0

D = (-5)² - 4·(-5) = 25 + 20  = 45

;

• (x² - 5x) = -6

x² - 5x + 6 = 0

D = (-5)² - 4·6 = 25 - 24 = 1

;

ответ: x =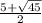   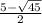; ; 3 ; 2