1. Алгебра
  2. Решите в натуральных числах

Решите в натуральных числах систему уравнений

{x+y+z=14;
{x+yz=19.
В качестве ответа введите количество решений и все возможные значения x.
Количество решений:

все значения х:

полинаполига полинаполига    3   27.06.2021 14:24    17

Ответы
Марта09 Марта09  27.07.2021 15:10

\displaystyle\bf \left \{ {{x+y+z=14} \atop {x+yz=19}} \right. =\left \{ {{19-yz+y+z=14} \atop {x=19-yz}} \right. = \\\\\\\left \{ {{(1-z)y+z-1=-5-1} \atop {x=19-yz}} \right. =-(z-1)y+(z-1)=-6\\\\\\(1-y)(z-1)=-6= \\\\1)\left \{ {{1-y=-1} \atop {z-1=6} \right. =y_1=2\quad;\quad z_1=7 \quad ; \quad \boxed{x_1=5}\\\\\\2)\left \{ {{1-y=-6} \atop {z-1=1}} \right. 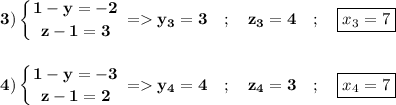= y_2=7 \quad ; \quad z_2=2 \quad; \quad \boxed{x_2=5}                                                                                                                                                                 \displaystyle\bf \\\\3)\left \{ {1-{y=-2} \atop {z-1=3}} \right. = y_3=3 \quad; \quad z_3=4 \quad ;\quad \boxed{x_3=7} \displaystyle\bf\\ \\\\4)\left \{ {1-{y=-3} \atop {z-1=2}} \right. = y_4=4 \quad; \quad z_4=3 \quad ;\quad \boxed{x_4=7}                                                                                                                                                                      В итоге система  имеет 4-решения  ; и так же 2 различных значения которые может принимать x это 7  и 5                                                                                                                                                    

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
20071218hi 20071218hi  09.03.2019 08:50
Известно, что f(x)=3x^2 + 2x -1. докажите что : f(sinx)=2sinx - 3cos^2x +2...
89051330939 89051330939  09.03.2019 08:50
Дорога длиной 10км от туристического лагря до поселка идет сначала под гору, а затем в гору. турист на спуске идет со скоростью,на 3 км/ч больше, чем на подъеме. путь от лагеря до...
nastya02012007 nastya02012007  09.03.2019 08:50
Требуется на 100 рублей купить 40 почтовых марок – рублевых, четырехрублевых, двенадцатирублевых. сколько окажется марок каждого достоинства? найти наименьшее натуральное число,...
tomchakd tomchakd  09.03.2019 08:50
чётко объяснить как правльно отбирать корни на тригонометрической окружности.(с1)...
DdMirko DdMirko  09.03.2019 08:50
Х^2+2x-15 0 решите неравенство методом интервалов...
baranovkirill baranovkirill  09.03.2019 08:50
Найдите площадь прямоугольника, вершины которого заданы координатами в декартевой системе координат а(0; -2), в(1; 0), с(7; -3), d(6; -5). ответ получается 15...
nigar26 nigar26  09.03.2019 08:50
Впервом мешке в 2 раза больше муки, чем во втором. когда из первого мешка взяли30 кгмуки, а во второй добавили5 кг, то во втором стало муки в 1,5 раза больше, чем в первом. сколько...
Руфина157 Руфина157  13.05.2020 18:58
При каких значениях параметра b сумма корней будет равна 11? ​...
Ramble2285 Ramble2285  13.05.2020 18:49
А) е основанием а; 6) е основанием аПредставьте в виде степени с основанием x частноа) : :в) – 1:х, где n – целое число;E) тех, где я — делое число.в тростите выгражение​...
Vadim55554 Vadim55554  13.05.2020 18:49
Округлите до тысячных число 6 538,6125...

Популярные вопросы