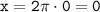Решите уравнение. 3cos^2x+cosx-4=0 на промежутке [ 0; п ] .
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему пищевой сахар не дает реакцию серебряного зеркала, а инвертированный...
3 - Решить : на диске записана информация в 3 файлах. на первый и второй приходится...
3 - Выражение: (3х-18)- (5х+14) 3(4-5х)-5(2х-8)...
1 - 1)10-3x=1 2)(x+1)+x=7 3) 5x: 2-10=-20 4)8-4x: 2=12...
2 - Л. лексика. 1. выберите соответствующее значение для выделенного слова:...
3 - 1)где в основном воды гидросферы? 2)назовите основные части мирового океана?...
2 - Объясните знаки препинания 1) татьяна ( душою, сама не зная почему) с...
1 - Укажите номера предложений, сказуемые которых стоят в prezent indefinite...
2 - По какому правилу составлены равенства : 7*5=35 14*5=70 28*5=140 56*5=280...
1 - Взаимодействия заряженных частиц . объяснение электализаци тел на основе...
1
Данное уравнение сводится к квадратному уравнению, поэтому сделаем замену:
Пусть cosx = t , но | t | ≤ 1
D = b² - 4ac = 1² - 4 × 3 × ( - 4 ) = 1 + 48 = 49 = 7²
t = ( - 1 ± 7 ) / 6
1) t = - 4 / 3 - не подходит по условию | t | ≤ 1
2) t = 1 - подходит
Обратная замена:
n принадлежит Z
На промежутке [ 0 ; π ] подходит только х = 0
ОТВЕТ: 0
Пусть при этом
при этом  , получим квадратное уравнение относительно t
, получим квадратное уравнение относительно t
Обратная замена:
Отбор корней на промежутке [0;π].
Если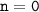 , то
, то