Решите подробно и с вычислениями : не просто график и второе задание

Ответы

avetik04 15.10.2020 16:07

ответ: $\left[-5;-\dfrac{7+2\sqrt{7}}{3}\right)\cup\left(-\dfrac{7+2\sqrt{7}}{3};-\dfrac{7}{2}\right)\cup\left(-1;-\dfrac{1}{2}\right]\cup\left\{\dfrac{-11+4\sqrt{7}}{9};\dfrac{7-2\sqrt{7}}{3};\dfrac{7+2\sqrt{7}}{3}\right\}$ Объяснение:

Исходная дробь равносильна следующей системе (числитель равен нулю, знаменатель не равен нулю + ОДЗ):

$\begin{cases}((|x|+|y|)^2-8(|x|+|y|)+15)(x^2+y^2-16)=0,\\ \sqrt{2x+y-1}\neq 0,\\ 2x+y-1\geq 0 \end{cases}$

В первом уравнении произведение равно нулю, когда хотя бы один из множителей равен нулю. Второе неравенство равносильно тому, что подкоренное выражение не равно нулю. Значит, вместе второе и третье образуют неравенство 2x + y - 1 > 0 ⇔ y > -2x + 1. Вернёмся к первому уравнению:

$\displaystyle\left [ {{(|x|+|y|)^2-8(|x|+|y|)+15=0,} \atop {x^2+y^2-16=0}} \right.$

В первом уравнении сделаем замену |x| + |y| = t.

t^2-8t+15=0

По теореме Виета $\displaystyle\left \{ {{t_1+t_2=8,} \atop {t_1t_2=15}} \right. \Rightarrow t_1=3,t_2=5$

Получаем $\left[\begin{gathered}|x|+|y|=3,\\|x|+|y|=5,\\ x^2+y^2=16\end{gathered}\right.$

Третье уравнение — уравнение окружности с центром (0; 0) и радиусом 4. Первые два уравнения — уравнения квадратов с центром в точке (0; 0), наклонённых на 45° и диагоналями 6 и 10: действительно, если раскрыть модуль y, а всё без y перенести в правую сторону, то при y ≥ 0 y = -|x| + 3, при y < 0 y = |x| - 3. Аналогично с |x| + |y| = 5.

Учтём ограничение y > -2x + 1: нам подохдят все y, что выше прямой -2x + 1. Всё вместе это выглядит, как на первой картинке. Теперь нужно обрезать всё, что не попадает в синюю область (см. вторую картинку).

Для выполнения второго задания вычислим точки пересечения квадратов и окружности с прямой y = -2x + 1, а также точки пересечения окружности и большого квадрата.

|x|+|1-2x|=3

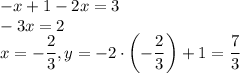
При x < 0: $-x+1-2x=3\\-3x=2\\x=-\dfrac{2}{3}, y=-2\cdot\left(-\dfrac{2}{3}\right)+1=\dfrac{7}{3}$

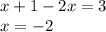При 0 ≤ x < 0,5: $x+1-2x=3\\x=-2$ — не подходит

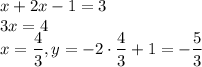
При x ≥ 0,5: $x+2x-1=3\\3x=4\\x=\dfrac{4}{3},y=-2\cdot \dfrac{4}{3}+1=-\dfrac{5}{3}$

|x|+|1-2x|=5

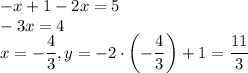
При x < 0: $-x+1-2x=5\\-3x=4\\x=-\dfrac{4}{3}, y=-2\cdot\left(-\dfrac{4}{3}\right)+1=\dfrac{11}{3}$

При 0 ≤ x < 0,5: $x+1-2x=5\\x=-4$ — не подходит

При x ≥ 0,5: $x+2x-1=5\\3x=6\\x=2,y=-2\cdot 2+1=-3$

$x^2+(1-2x)^2=16\\x^2+1-4x+4x^2-16=0\\5x^2-4x-15=0\\D_{/4}=2^2+5\cdot 15=79\\x_1=\dfrac{2+\sqrt{79}}{5},y_1=-2\cdot\dfrac{2+\sqrt{79}}{5}+1=\dfrac{1-2\sqrt{79}}{5}\\x_2=\dfrac{2-\sqrt{79}}{5},y_2=-2\cdot\dfrac{2-\sqrt{79}}{5}+1=\dfrac{1+2\sqrt{79}}{5}$

$\displaystyle\left \{ {{|x|+|y|=5,} \atop {x^2+y^2=16}} \right.\left \{ {{|x|+\sqrt{16-x^2}=5,} \atop {|y|=\sqrt{16-x^2}}} \right.$

Решим первое уравнение:

$\sqrt{16-x^2}=5-|x|\\16-x^2=25-10|x|+x^2\\2x^2-10|x|+9=0\\0\leq x\leq 5: 2x^2-10x+9=0\\D_{/4}=5^2-2\cdot 9=7\\x_1=\dfrac{5-\sqrt{7}}{2},y_1=\pm\sqrt{16-\left(\dfrac{5-\sqrt{7}}{2}\right)^2}=\pm\sqrt{\dfrac{64-25+10\sqrt{7}-7}{4}}=\\=\pm\dfrac{\sqrt{25+10\sqrt{7}+7}}{2}=\pm\dfrac{5+\sqrt{7}}{2}\\x_2=\dfrac{5+\sqrt{7}}{2},y_2=\pm\dfrac{5-\sqrt{7}}{2}$

$-5\leq x$

Прямая y = px - 1 — прямая, проходящая через точку (0; -1). Действительно, если подставить x = 0, вне зависимости от параметра p при данном x y = -1. p регулирует наклон прямой. Будем вращать прямую около точки (0; -1) и отмечать промежутки (красным), где прямая "начинает" и "заканчивает" иметь две общие точки (см. третью картинку).

На рисунке отмечены все промежутки и частные случаи, когда прямая имеет две общие точки. Выразим p через x и y:

$y+1=px\\p=\dfrac{y+1}{x}$

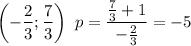
Для $\left(-\dfrac{2}{3};\dfrac{7}{3}\right)\ p=\dfrac{\frac{7}{3}+1}{-\frac{2}{3}}=-5$

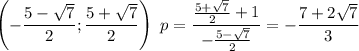
Для $\left(-\dfrac{5-\sqrt{7}}{2};\dfrac{5+\sqrt{7}}{2}\right)\ p=\dfrac{\frac{5+\sqrt{7}}{2}+1}{-\frac{5-\sqrt{7}}{2}}=-\dfrac{7+2\sqrt{7}}{3}$

Для $\left(-\dfrac{4}{3};\dfrac{11}{3}\right)\ p=\dfrac{\frac{11}{3}+1}{-\frac{4}{3}}=-\dfrac{7}{2}$

Для $\left(2;-3\right)\ p=\dfrac{-3+1}{2}=-1$

Для $\left(\dfrac{4}{3};-\dfrac{5}{3}\right)\ p=\dfrac{-\frac{5}{3}+1}{\frac{4}{3}}=-\dfrac{1}{2}$

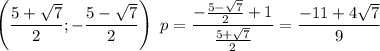
Для $\left(\dfrac{5+\sqrt{7}}{2};-\dfrac{5-\sqrt{7}}{2}\right)\ p=\dfrac{-\frac{5-\sqrt{7}}{2}+1}{\frac{5+\sqrt{7}}{2}}=\dfrac{-11+4\sqrt{7}}{9}$

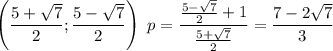
Для $\left(\dfrac{5+\sqrt{7}}{2};\dfrac{5-\sqrt{7}}{2}\right)\ p=\dfrac{\frac{5-\sqrt{7}}{2}+1}{\frac{5+\sqrt{7}}{2}}=\dfrac{7-2\sqrt{7}}{3}$

Для $\left(\dfrac{5-\sqrt{7}}{2};\dfrac{5+\sqrt{7}}{2}\right)\ p=\dfrac{\frac{5+\sqrt{7}}{2}+1}{\frac{5-\sqrt{7}}{2}}=\dfrac{7+2\sqrt{7}}{3}$

Итого

$p\in\left[-5;-\dfrac{7+2\sqrt{7}}{3}\right)\cup\left(-\dfrac{7+2\sqrt{7}}{3};-\dfrac{7}{2}\right)\cup\left(-1;-\dfrac{1}{2}\right]\cup\\\cup\left\{\dfrac{-11+4\sqrt{7}}{9};\dfrac{7-2\sqrt{7}}{3};\dfrac{7+2\sqrt{7}}{3}\right\}$