Найдите наименьшее натуральное число, которое при умножении на 2 становится точным квадратом, а при умножении на 3 – точным кубом.
Ответы
Наше число будем искать в виде 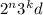 , где
, где 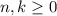 ,
, 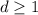 и
и  не делится ни на 2 ни на 3. Заметим, что любое натуральное число можно представить в таком виде. Тогда по условию
не делится ни на 2 ни на 3. Заметим, что любое натуральное число можно представить в таком виде. Тогда по условию  должно быть квадратом, а
должно быть квадратом, а  должно быть кубом, т.е.
должно быть кубом, т.е. 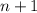 и
и 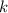 делятся на 2, а
делятся на 2, а 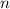 и
и 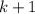 делятся на 3, и, кроме того,
делятся на 3, и, кроме того,  является одновременно и квадратом и кубом, т.е. является 6-ой степенью. Минимальное
является одновременно и квадратом и кубом, т.е. является 6-ой степенью. Минимальное 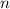 , такое что оно делится на 3 и
, такое что оно делится на 3 и 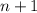 делится на 2 равно 3, т.е.
делится на 2 равно 3, т.е.  . Минимальное
. Минимальное 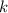 , такое что оно делится на 2 и
, такое что оно делится на 2 и 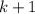 делится на 3 равно 2, т.е.
делится на 3 равно 2, т.е. 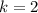 . Минимальное
. Минимальное  , которое является 6-ой степенью равно 1. Итак, искомое число равно
, которое является 6-ой степенью равно 1. Итак, искомое число равно  . ответ: 72.
. ответ: 72.
ПОКАЗАТЬ ОТВЕТЫ
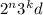 , где
, где 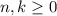 ,
, 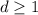 и
и  не делится ни на 2 ни на 3. Заметим, что любое натуральное число можно представить в таком виде. Тогда по условию
не делится ни на 2 ни на 3. Заметим, что любое натуральное число можно представить в таком виде. Тогда по условию  должно быть квадратом, а
должно быть квадратом, а  должно быть кубом, т.е.
должно быть кубом, т.е. 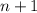 и
и 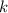 делятся на 2, а
делятся на 2, а 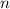 и
и 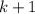 делятся на 3, и, кроме того,
делятся на 3, и, кроме того,  является одновременно и квадратом и кубом, т.е. является 6-ой степенью. Минимальное
является одновременно и квадратом и кубом, т.е. является 6-ой степенью. Минимальное 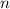 , такое что оно делится на 3 и
, такое что оно делится на 3 и 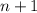 делится на 2 равно 3, т.е.
делится на 2 равно 3, т.е.  . Минимальное
. Минимальное 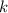 , такое что оно делится на 2 и
, такое что оно делится на 2 и 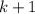 делится на 3 равно 2, т.е.
делится на 3 равно 2, т.е. 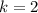 . Минимальное
. Минимальное  , которое является 6-ой степенью равно 1. Итак, искомое число равно
, которое является 6-ой степенью равно 1. Итак, искомое число равно  . ответ: 72.
. ответ: 72.
Другие вопросы по теме Алгебра
Популярные вопросы
- Дайте означення кола, радіуса кола, хорди кола, діаметра кола....
3 - Определить количество теплоты, необходимое для плавления 4 кг алюминия,...
1 - Замени t одночленом так, чтобы получился квадрат бинома....
3 - Ширина прямокутника на 12 см більша ніж довжина. Знайти площу і сторони...
2 - Спів соловейка - це приклад поведінки *соціальноїрепродуктивноїгігієнічноїнабуто...
3 - Вычислите естественный прирост населения. Рождаемость составила 23 человека...
1 - Кауфман 5 класс Lister to the text and answer the guestijns. 1 Wat are...
2 - ОООЧЕНЬ Читати твір Неймовірні пригоди Івана Сили , скласти з першого по...
3 - Пришёл Батый к Киеву с большой силой, с многим множеством воинов. Был Батый...
3 - Какие типы гамет могу образовывать организмы со следующим сочитанием генов...
3