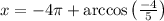Решите . под буквой "б" объясните а) 5cosx + 4/ 4tgx -3 =0 б) [-4п; -5п/2 ]
Другие вопросы по теме Алгебра
Популярные вопросы
- . В автобусе 30 мест. Сколькими можно рассадить 6 человек, при...
2 - Студенты первого курса в сессию сдают два экзамена :по математике...
2 - Суммой двух событий называется:...
2 - Математическое ожидание нормально распределённой случайной величины...
1 - РЕШИТЕ В каждом мешочке находится 9 белых шаров и 1 черный. Юноша...
3 - Составить календарь проведения спортивных соревнований по баскетболу...
2 - Нажмите первообразную следующих функций:...
2 - решить. Здесь два задания....
3 - Электрон в невозбужденном атоме водорода получил энергию E=12,75...
1 - получите суспензию BaSo4 всеми возможными Покажите строение частиц...
1
А)
Если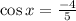 , то для х ∈ 3ч. :
, то для х ∈ 3ч. :
Значит на тригонометрической окружности точки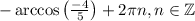 и
и 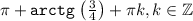 совпадают, поэтому решением системы будет
совпадают, поэтому решением системы будет 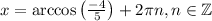
Б)
На промежутке [0;2π] корнем системы будет: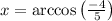
Значит на промежутке [-4π;-2π] корень будет: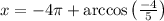
Заданный в условии промежуток не ограничивает корень системы на промежутке [-4π;-2π].
ответ: А)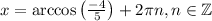
Б)