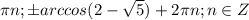Решите очень
2sin2x+sin^3x=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Впайтоне. нужно написать код и объяснить. задається деякий текст, що зберігається...
2 - Ломаю голову как закончить реакцию. ch3-ch2-c≡ch + ch3-ch2-mgbr = по идеи,...
3 - Как называется тепловая обработка мяса в духовом шкафу? ...
2 - сильно о ! условие определите знак числа, если известно,что число a отрицательное....
3 - Основные рудные ресурсы их размещение и крупнейшие месторождения . решить...
2 - Напишіть будь ласка риси характеру чумака та купця у гуморесці добре торгувалось...
2 - Какой объем воздуха уйдет на окисление гидроксида железа,полученного при...
1 - 3) найдите разницу арифметической прогрессии an если a1 =5 и a3=15...
3 - Укажите значение у в решении уравнениясостоящем из натуральных чисел.x+1/y+1/z...
3 - Скорее будет 20: 299: 9972: 912: 310: 545: 981: 9...
1
или
ответ: