Решите нееравенство 8 класса.
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите сочинение 15 предложений на тему как я хожу в школу с выполненными...
3 - вообще не знаю как сделать...
1 - ПОМАГИТЕЕЕ Астана-арман қалаатты тақырыпқа мəтін қура (составьте расказ 6-7)...
2 - Написать программу, которая выводит все числа не превышающие заданного числа...
1 - Создайте эскиз (рисунок) вашего будущего изделия в цвете. ...
3 - 6. У якому рядку всі слова пишемо з апострофом? AЛук..янець, звязкiвець, мавп..ячий,...
3 - Протокол прл школи на будь яку яку тему.. Будьласка...
1 - 3. Найди в тексте ответ на вопрос заголовка. 5все3. СТЫСЧто вредит воздуху?Людям...
3 - Вычислите 0,8*0,2=ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ...
1 - 7. Жөнөкөй жана тутумдаш баяндоочторду өз-өзүнчө топторго бөлүп жазгыла: жардам...
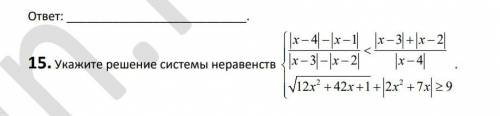
2
Объяснение:
Решим первое неравенство. ОДЗ:
Если x < 1 или x ≥ 4, то модули раскрываются с одним знаком, произведение подмодульных выражений положительно:
Учитывая, что x < 1 или x ≥ 4, а также учитывая ОДЗ,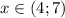
Если 1 ≤ x < 4, то модули раскрываются с разным знаком, произведение подмодульных выражений отрицательно:
Учитывая, что 1 ≤ x < 4 и ОДЗ, .
.
Объединяя полученные промежутки, получаем, что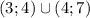
Решим второе неравенство. Пусть . Тогда
. Тогда
Если правая часть отрицательна, то неравенство выполняется на ОДЗ, так как квадратный корень всегда неотрицателен:
Если правая часть неотрицательна, то обе части можно возвести в квадрат:
Если t ≥ 0, то модуль раскрывается с плюсом, первое неравенство имеет вид:
Если t < 0, то модуль раскрывается с минусом, неравенство имеет вид:
Сумма неотрицательного и положительного чисел не может быть неположительной. В данном случае решений нет.
Учитывая -9 ≤ t ≤ 9, решением данного случая является![t\in[4;9]](/tpl/images/1358/7181/70120.png)
Объединив оба случая, получаем t ≥ 4,
Пересечём полученные решения: ответом будет