1. Алгебра
  2. Решите квадратное уравнение: а)

Решите квадратное уравнение: а) х квадрат-х-30=0; б) 5х квадрат-7х+2=0

BOG5555 BOG5555    3   03.03.2019 06:00    2

Ответы
UILA336 UILA336  23.05.2020 23:21

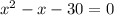
а) x^{2}-x-30=0

 

Квадратное уравнение имеет вид: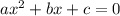 ax^{2}+bx+c=0

 

Cчитаем дискриминант:

 

D=b^{2}-4ac=(-1)^{2}-4\cdot1\cdot(-30)=1+120=121

 

Дискриминант положительный

 

\sqrt{D}=11

 

Уравнение имеет два различных корня:

 

x_{1}=\frac{-b+\sqrt{D}}{2a}=\frac{1+11}{2\cdot1}=\frac{12}{2}=6

 

x_{2}=\frac{-b-\sqrt{D}}{2a}=\frac{1-11}{2\cdot1}=\frac{-10}{2}=-5

=======================================================

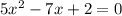
б) 5x^{2}-7x+2=0

 

Cчитаем дискриминант:

 

D=(-7)^{2}-4\cdot5\cdot2=49-40=9

 

Дискриминант положительный

 

\sqrt{D}=3

 

Уравнение имеет два различных корня:

 

x_{1}=\frac{7+3}{2\cdot5}=\frac{10}{10}=1

 

x_{2}=\frac{7-3}{2\cdot5}=\frac{4}{10}=0,4

ПОКАЗАТЬ ОТВЕТЫ
inber657205 inber657205  23.05.2020 23:21

1)х^2-х-30=0 

по т виета

Х1+Х2=1

Х1*Х2=-30

х1=6

х2=-5

 

2)5х^2-7х+2=0

D=49-4*5*2=9

х1= (7+3)/10=1

х2=(7-3)/10=0,4

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
shuraKotokoto shuraKotokoto  22.09.2019 13:50
Вычислите значение выражения 9^1+log9 5...
soynova89 soynova89  22.09.2019 13:50
Змей длиной 110 м спросонья ползёт по трубе со скоростью 1 км/ч. навстречу змею по этой трубе бежит белка со скоростью 10 км/ч, опаздывая на урок по зельеварению. белка вскочила...
Darvin2004 Darvin2004  22.09.2019 13:50
1) найди трёхзначное число,равное кубу суммы его цифр 2) к числу 43 припишите слева и справа по одной цифре так, чтобы полученное число делилось на 45 3) электронные часы показывают...
Sss5555500 Sss5555500  22.09.2019 13:50
Установите при каких значениях переменной не имеет смысла дробь 1)a-5/a+5, 2)5c/4+10c, 3)3x-9/1+x, 4) 15m+4/4m+15...
ksenia1716 ksenia1716  22.09.2019 13:50
Cosa=-1/2, pi3pi/2. найдите sin(30+a) , с решением...
алёнааепар алёнааепар  21.02.2021 12:45
Дано cos a = -2/3 180найти sin a, tg a, ctg a, sin 2 a, sin a/2a-это альфа...
мороженле мороженле  21.02.2021 12:48
Разложи на множители (x+5y)^2−(5x+y)^2 . (Найди конечное разложение, в котором каждый множитель уже нельзя разложить на множители!) Выбери правильный ответ: 1. (x2+25y2)⋅(25x2+y2)...
bceznaika2 bceznaika2  21.02.2021 12:51
Дифференцированные задания по уровням А. 1) 7а - 7в + аn – bn 2) xy + 2y + 2x + 4 3) y2a - y2b + x2a - x2b Б. 1) xy + 2y - 2x – 4 2) 2сх – су – 6х + 3у 3) х2 + xy + xy2 + y3 С....
Yury28 Yury28  02.03.2020 16:58
пошагово для тупых:-7\3-14​...
нрпаллмаегли нрпаллмаегли  02.03.2020 16:58
1. 3х-7=4(2х-3)-5 2. 17-2(6х-5)=4(7х-2) 3. 6х-3(5х+4)-2(7х-3)= -6 4. -2(х+21)-3(х-14)= -5х...

Популярные вопросы