Решить задание из прикрепленного файла.
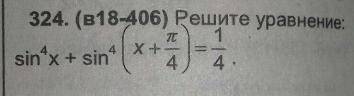
Другие вопросы по теме Алгебра
Популярные вопросы
- У покупателя было 10 000 сумов. Он купил 3 kg яблок по 1 900 сумов и по...
3 - В каких поступках проявились честь, достоинство, благородство героя(Петр...
2 - 2. На рисунку зображено графік функції = f (x). Знайдіть f(-2), f (0)...
1 - Каков алгоритм определения вида придаточной части? . Что обозначает придаточная...
1 - «Серед іншого я казав,— розповідав в’язень,— що будь-яка влада є насильством...
3 - Распредили основные задачи развития системы образования по первым пятилеткам...
2 - Задание 1. Напишите диктант, вставьте пропущенные буквы и расставьте знаки...
1 - 2. Какой вид террора в настоящее время вышел на первое место в мире по...
2 - перевести с русского на английский текст: Семья Симпсонов — вымышленная семья...
2 - Почему Ашик-Кериб забыл о своей возлюбленной Магуль-Мегери?...
2
x = π*n , n∈Z
x = -π/4 +π*k , k∈Z
Объяснение:
Используем формулу понижения степени :
sin^2(t) = (1-cos(2t) )/2
( (1-cos(2x) )/2)^2 + ( ( 1-cos(2x +π/2) )/2)^2 = 1/4
Умножаем на 4 обе части уравнения, учитывая, что
cos(2x +π/2) = -sin(2x)
(1-cos(2x) )^2 +(1+sin(2x) )^2 = 1
1 -2*cos(2x) +cos^2(2x) +1+2*sin(2x) +sin^2(2x) = 1
Поскольку : cos^2(2x)+sin^2(2x) = 1
-2*cos(2x)+2*sin(2x) = -2
cos(2x) -sin(2x) = 1
√2/2 *( cos(2x) -sin(2x) ) =√2/2
cos(2x+π/4) = √2/2
2x+π/4 = +-π/4 +2*π*n , n∈Z
x+π/8 = +-π/8 +π*n, n∈Z
x = π*n , n∈Z
x = -π/4 +π*k , k∈Z