Популярные вопросы
- Какая сила действует на электрон в электрическом поле с напряженностью 0,6...
2 - Скакой высоты надо бросить тело, чтобы оно упало на землю со скоростью 30...
3 - 8+2+4+5=30 найдете заблудившиеся цифры и поменяйте местами...
2 - Тело бросили с поверхности земли с начальной скоростью 20 м/с. найдите максимальную...
3 - Make up sentences. 1. never/ he/ his wife’s birthday/ forgets. 2. usually...
1 - Имеется 5 литровый и 9 литровый сосуды как набрать из реки 3 литра воды,сделав...
2 - Какие насекомые эволюционно давнее- с полным или неполным превращением в цикле...
2 - 7.высота цилиндра равна 4 м, расстояние между осью цилиндра и параллельной...
2 - Что такое производные предлоги в языке?...
3 - Знайти інтервали монотонності функції у=x^2-6x+5...
2
Пусть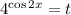 при этом должно выполнено условие
при этом должно выполнено условие 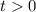 , получим:
, получим:
По теореме Виета
Возвращаемся к обратной замене: