решить уравнение с параметром

Если a∈(0;1|, то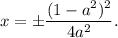   При прочих a решений нет.

Объяснение:

Поскольку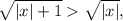  делаем вывод, что a>0. Кроме того, функция  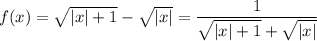четная (f(-x)=f(x)) и при x>0 убывающая. Поэтому самое большое значение эта функция достигает при x=0, и это значение равно 1. Поэтому для a можно сделать и такое ограничение: a≤1. Пока мы не знаем, как эти рассуждения нам жить, но хуже точно не будет. Итак,                  a∈(0;1].

Обозначим:

Заметим, что

  p²-q²=|x|+1-|x|=1, поэтому для нахождения p и q имеем систему

Кстати, то, что a∈ (0;1), мы использовали при возведении в квадрат второго уравнения системы.