Решить уравнение (логорифмы)
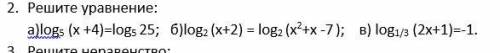
Другие вопросы по теме Алгебра
Популярные вопросы
- Пусть имеется n=5 чисел (1,2,3,4,5). Найти 93-ю перестановку. ответ...
3 - Какое количество 10% раствора соли надо добавить к 200 г. 40% раствора,...
1 - с задачей. Рон Уизли купил себе сверхскоростную метлу. После этого...
3 - 11. Речення, у якому наявні всі необхідні для розуміння змісту члени...
1 - . Найдите область определения функции. Фото прилагаю.Заранее нужно!...
2 - Почему кирпичи сушили на солнце?...
1 - Физика 8 класс Цена деления и предел измерения Рассмотри шкалу прибора....
3 - В магазин привезли 66 кг чёрного и белого винограда в 2 коробках был...
1 - Замовник вибирає багатофункціональний пристрій для створення домашньої...
2 - Товар стоит 7000 рублей, но мне нужно что бы он стоил 5000 рублей....
2
Объяснение:
а) log₅ (x + 4) = log₅ 25
Область допустимых значений: (ОДЗ)
x + 4 > 0
x > - 4
"Опустим" логарифмы, так как у них одинаковые основания:
x + 4 = 25
x = 21
Это значение входит в ОДЗ, значит, мы получили ответ
б) log₂ (x + 2) = log₂ (x² + x - 7)
Здесь проще сразу опустить логарифмы, сделав в конце проверку для каждого корня:
x + 2 = x² + x - 7
2 = x² - 7
x² = 9
x = ±3
Для x = 3:
log₂ (3 + 2) = log₂ (9 + 3 - 7)
log₂5 = log₂5
Этот корень входит в решение.
Для x = -3
log₂ (-3 + 2) = log₂ (9 - 3 - 7)
log₂ (-1) = log₂ (-1)
Логарифма отрицательно числа не существует, значит, x = -3 не является корнем уравнения:
ответ: x = 3
в) log (1/3) (2x + 1) = -1
ОДЗ: 2x + 1 > 0
2x > - 1
x > -1/2
Вынесем степень -1 из одной третьей:
-log₃ (2x + 1) = -1
log₃ (2x + 1) = 1
Представим единицу как log₃3 и опустим логарифмы:
log₃ (2x + 1) = log₃3
2x + 1 = 3
2x = 2
x = 1
Этот корень входит в ОДЗ, значит, это наш ответ