Решить уравнение
3/sin(x) - 2/cos(x) = sqrt(52).
с решением.
Другие вопросы по теме Алгебра
Популярные вопросы
- Алтын орданың мемлекеттік циклін зерттеу...
2 - Как называется летопись монголов, в которой описывается быт, традиции монголов? *...
3 - 8 -тапсырма.«Қосжазба күнделігі». Мәтін мазмұнынасүйеніп, үш тұжырымға түсініктеме...
2 - НУЖНО СОСТАВИТЬ МОЕ ОТНОШЕНИЕ К БАРЫНЕ В ЭПИЗОДЕ С МУМУ МИНИМУМ 10 ПРЕДЛОЖЕНИЙ...
2 - Текст на тему что значит любовь 70 слов...
2 - Қазақ әдебиеті 1,2тапсырма 104бет 5сынып...
1 - ответы на вопросы 1.Что такое переменная?2Из чего состоит имя переменной?3.Перечислите...
1 - Спрогнозируйте свойства химических элементов: рубидия (Rb), брома (Br) по положению...
1 - 9.1 Укажите слова состав которых соответствует схеме корень + окончание a) хитрый...
2 - 8-тапсырма. «Биотехнология болашақтың ғылымы» деген пікірменкелісесің бе? Пікіріңді...
2
Объяснение:
Пусть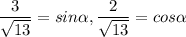
Тогда
Воспользуемся формулами
Тогда уравнение принимает вид:
Найдем α из одного из условий
Тогда получим