Решить неравенство: 4^x -3*2^x -4< 0
Другие вопросы по теме Алгебра
Популярные вопросы
- Коэффициент жёсткости пружины 320 Н/м. На сколько сантиметров нужно...
1 - Лист до дядька шпичака з твору лось...
2 - В приведённом фрагмене кода на языке Pascal выберите страну, являющуюся...
1 - Составить задачу на нахождение процента от числа...
3 - Үлкен кісілерден жиі еститін «Ата бабасының қанына тартқан» деген...
2 - С каким животным пришлось бороться золотоискателю?( : 1)гиеноймедведемвепремволком...
2 - решить матешу 6 класс контрольная...
3 - Вкладник вніс до банку 5000 грн під певні відсотки річних, і через2...
3 - Дописати схеми реакції та перетворити їх на хімічне рівняння. Для...
1 - 2. Установите соответствиеА) Капиталистический стройB) феодальній...
1
Пусть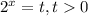 , тогда
, тогда
Получили, что
Так как 2 > 1, то x < 2,
x∈ (- ∞ ; 2).
ответ: (- ∞ ; 2).
4^x -3*2^x -4<0
2^(2x) -3*2^(x) -4<0
замена 2^x =а ОДЗ а>0
а²-3а-4<0
D=9+16=25
a=(3+5)/2=4 2^x =4 х=2
a=(3-5)/2=-1 не подходит под ОДЗ
- +
2
х∈(-∞;2)