Решить логарифмические уравнения
Другие вопросы по теме Алгебра
Популярные вопросы
- Визначте потужність двигуна автомобіля, якщо витрати бензину становлять 38 л на...
3 - В 16 веке Нидерландские провинции находились под властьюА. АнглииБ. ФранцииВ. ИспанииГ....
2 - Фантастическая одежда в сказке заколдованное место Закалдованное Место» Гоголь...
2 - надо сдать до Какие виды деформаций изображены на рис. 3.35?...
2 - За перший день було скошено луків. Яку площу луків було скошено другого дня , якщо...
2 - Какой итог Восстание Касыма Абылайулы и Саржана Касымулы ...
1 - 9. Рухаючись трасою Житомир Чернівці, автомобіль відстань між 237та 239-кілометровими...
2 - Какие пословицы и поговорки связаны с понятием митоза?...
2 - по какому нибудь номеру, или две если можете...
1 - 1. Расставь знаки препинания в предложениях, которые даны в документе. 2. Определи...
3
1)
ОДЗ: x>0
Замена:
Обратная замена:
ответ: {e; e²}
ОДЗ: x²+3x-1>0
x∈(-∞;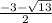 )∪(
)∪(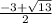 ;+∞)
;+∞)
ответ: {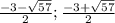 }
}