Алгебра: решить хоть какой , люди добрые

решить хоть какой
, люди добрые

решить хоть какой , люди добрые

Ответы

ALEXIA24 10.01.2022 12:18

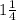3. $1\frac{1}{4}$ (ответ (2))

4. (ответ (3))

5....

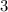
Объяснение:

Найти абсциссу точки пересечения - это, по сути, найти координату х точки пересечения (т.к. для функции у=32 значение у постоянно и не зависит от значения х, а функция у=16^х непрерывна и монотонно возрастает на всей области определения, такая точка единственная)

А значение х в этой точке - это по сути корень уравнения: 16^х= 32

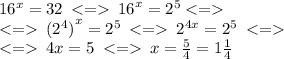
$16^{x} = 32 \: < = \: {16}^{x} = {2}^{5} < = \\ < = \: {( {2}^{4} )}^{x} = {2}^{5} \: < = \: {2}^{4x} = {2}^{5} \: < = \: \\\: < = \: 4x = 5 \: < = \: x = \frac{5}{4} = 1\frac{1}{4}$

$2 \cdot3^{x + 1} - 9\cdot3^{x - 1}= 9 \\ 2 \cdot3^{x + 1} - {3}^{2} \cdot3^{x - 1}= 9 \\ 2 \cdot3^{x + 1} - 3^{2 + (x-1)}= 9 \\ 2 \cdot3^{x + 1} - 3^{x +1}= 9$

Замена переменной (хотя можно и без неё):

$t = {3}^{x + 1}$

$2 {t}- t= 9 \\ t = 9 \\ t = {3}^{2}$

Обратная замена:

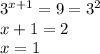
${3}^{x + 1} = 9 = {3}^{2} \\ x + 1 = 2 \\ x = 1$

${9}^{x} - {75} \cdot3^{x - 1} - 54 = 0 \\ {( {3}^{2} )}^{x} - {75} \cdot3^{x }\cdot3^{ - 1 } - 54 = 0 \\ {3}^{2x} - \frac{ ^{25} \: \cancel{75} \cdot3^{x } }{ \cancel{ \: 3 \: }} - 54 = 0 \\ {3}^{2x} - 25\cdot3^{x } - 54 = 0$

Замена переменной:

$t = {3}^{x} \: = \: \: {3}^{2x} = {t}^{2} \\$

Получаем квадратное уравнение, которое решим по Т. Виета

t^2-25t-54=0

По Т. Виета

$\left[ \begin{array}{l}t_{1} + t_{2} = 25 \\t_{1} \times t_{2} = - 54 \\ \end{array} \right. = \left[ \begin{array}{l}t_{1} = 27 \\ t_{2} = - 2 \\ \end{array} \right.$

Обратная замена

$\left[ \begin{array}{l}t_{1} = 27 \\ t_{2} = - 2 \\ \end{array} \right. < = \left[ \begin{array}{l} {3}^{x} = 27 \qquad\qquad(1) \\ {3}^{x}= - 2 \: \: \: \: \: \: \: \qquad(2) \\ \end{array} \right.$