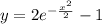Решить дифференциональное уравнение y`+xy+x=0 при x=0, при у=1
Другие вопросы по теме Алгебра
Популярные вопросы
- Давид бен-гурион 1. социальное происхождение. условия, в которых формировались...
2 - Итоги ускоренного развития в 18 веке в европе...
1 - Составить предложение со словом кемерово...
1 - Сузбекским 2-mashq. berilgan fe llarga i va ii shaxs-son qoʻshimchalarini...
3 - Биология. заполните таблицу. лабороторная работа №2...
3 - Напишите небольшое сочинение рассуждение на тему почему мы говорим что...
2 - Координата тела, движущегося прямолинейно и равномерно, изменяется по...
2 - 1/25 ×26 + 1/26 × 27 + 1/27 × 28 + 1/28 × 29 +1/29 × 30 решить в виде...
2 - Дан параллелограмм abcd со сторонами 6 и 5 и углом a=30 градусов. найдите...
3 - Знайти значення виразу ( √2-√5)^2+(√√5-3)^2...
1
Дифференциальное уравнение является уравнением с разделяющимися переменными.
Получили общее решение.
Найдем теперь частное решение, подставляя начальные условия
Частное решение: