Решить дифференциальное уравнение второго порядка y''+(y')^2+1=0)
Другие вопросы по теме Алгебра
Популярные вопросы
- все звуковык образы в светлана...
3 - с заданием. Начинающий. Язык С# 1) Написать метод, вычисляющий 5 x2+3 y2. С его...
1 - Что будет выведено на экран после выполнения фрагмента программы: begin a:=3;...
2 - Посчитайте стоимость потраченной электроэнергии (освещение, работа станков),...
2 - решить кроссворд 6 класс В учебнике этого задания нету...
1 - Биссектриса угла прямоугольника делит его сторону на отрезки длинной 4 см и 8...
3 - В треугольнике KPR проведена высота PD. Известно, что ∡ PKR = 18° и ∡ KPR = 128°....
2 - Үлгі: Зымыранды көргің келе ме? Қашан көргің келеді?Ғарыш туралы оқисың ба? Қашан...
1 - Подбери пословицы о смелости и отваге ( не менее 5) чем полезен страх и смелость...
1 - Какие процессы изучают генная и клеточная инженерия? Конструирование новых генов...
2
Понизим порядок заменой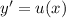 , тогда
, тогда 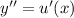 , получим
, получим
Выполнив обратную замену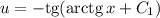 , получим
, получим
Тогда