Решить 3 тригонометрических 1). 3 sin²x +9sinx=0 2). sin²x-2sinx-3=0 3). cos²x-3sinx-3=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Choose the correct words. 1 I can t find my mp3 player. My brother...
3 - 1. Із поданого переліку речовин випишіть окремо формули електролітів...
1 - Рабочий за 8 часов изготовил 145 деталей. Сколько деталей он...
2 - Караганды көмір алабының ресурспен қамтамасыз етілуі...
2 - привіт, артеме чи привіт артем ?...
2 - напишите кратко, но развёрнуто таблицу...
3 - Сравнить числа х и у если: 1) у-х=-2/52) х-у=(-8)³3)у-х=0,34)х-у=-12²...
3 - В каком из нижеприведенных случаях в контуре не возникает ЭДС...
1 - тый клас всемирная история ...
3 - Что такое среда обитания Назови основные среды обитания Почему...
3
1). 3 sin^2x +9sinx=0
3sinx(sinx+3)=0
3sinx=0 -> x=pi*k
sinx+3=0 ->sinx= -3 - не существует
ответ: x=pi*k
2). sin²x-2sinx-3=0
D=4+12=16
sinx=3 - не существует
sinx= -1 -> x= -pi/2+2pi*k
ОТвет: x= -pi/2+2pi*k
3). cos^2x-3sinx-3=0
(1-sin^2x)-3sinx-3=0
sin^2x+3sinx+2=0
D=9-8=1
sinx= -2 - не существует
sinx= -1 => x= -pi/2+2pi*k
ОТвет: x= -pi/2+2pi*k
1) 3 sin²x +9sinx=0
Вынесем за скобку общий множитель:
3sinx(sinx+3)=0
Произведение равно 0, когда хотя бы один из множителей равен 0.
3sinx=0(по частным формулам) sinx+3=0
sinx=-3 (такого быть не может, т.к. синус принимает значения от -1, до : [-1;1])
ответ: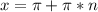
2) sin²x-2sinx-3=0
Это квадратное уравнение, обозначим sinx=a, a принимает значения [-1;1]
a²-2a-3=0
Корни находим по теореме Виета
a1=3 a2=-1
sinx=-1 ( по частным формулам)
3) cos²x-3sinx-3=0
По основной формуле заменим косинус( cos²x=1-sin²x) и получим квадратное уравнение:
1-sin²x-3sinx-3=0
sin²x+3sinx+2=0
sinx=a, a принимает значения [-1;1-]
a²+3a+2=0
a1=-2 a2=-1
sinx=-1