Суммативное оценивание № 1 за раздел «Функция, ее свойства и график»

Тема: Свойства функции.

Дробно – линейная функция.

Понятия сложной и обратной функции.

Цели обучения: 10.4.1.4.Уметь описывать по заданному графику функции её свойства: 1) область определения функции

2) область значения функции

3) нули функции

4) периодичность функции

5) промежутки монотонности функции

6) промежутки знакопостоянства функции

7) наибольшее и наименьшее значения функции

8) четность, нечетность функции

9) ограниченность функции

10) непрерывность функции

11) экстремумы функции

10.4.1.5. Определить свойства у=(ax+b )/(cx+d ),c≠0дробно-линейной функции и строить её график

10.4.1.6. Знать определение обратной функции и находить функцию, обратную заданной и знать свойство расположения графиков взаимно обратных функций

1 вариант1

Критерий оценивания

Исследует свойства функции по ее графику

Использует свойства и строит график дробно- линейной функции

Применяет алгоритм нахождения обратной функции

Уровень мыслительных навыков применение

Время выполнения 25 минут

1 вариант

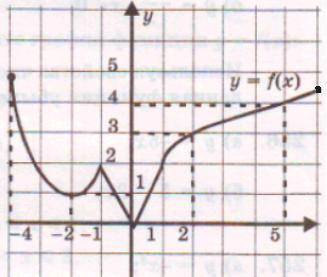
№1. Дан график функции.

а) Запишите область определения функции. ( )

б)Найдите множество значений функции. ( )

с)Определите максимальное значение функции на области определения; ( )

д)Определите четность функции. ( )

№2. Постройте график функции .

Выделите из рациональной дроби целую часть, выпишите коэффициенты;

Составьте таблицу значений для функции ; ( )

Найдите точки пересечения кривой с осями координат; ( )

Постройте график функции ( )

№3. а) Найдите обратную функцию для функции ; ( )

б) Как будет расположен график обратной функции относительно первоначальной? ( )

2 вариант

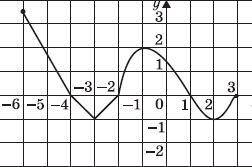
№1. Дан график функции.

Запишите область определения функции. ( )

Найдите множество значений функции. ( )

Определите максимальное значение функции на области определения; ( )

Определите четность функции ( )

№2. Постройте график функции .

Выделите из рациональной дроби целую часть, выпишите коэффициенты;

Составьте таблицу значений для функции ; ( )

Найдите точки пересечения кривой с осями координат; ( )

Постройте график функции ( )

№3. а) Найдите обратную функцию для функции ; ( )

б) Как будет расположен график обратной функции относительно первоначальной?

(

ДженниЛенни    1   29.10.2020 11:55    54