1. Алгебра
  2. Решать все 6 класс! решить уравнение

Решать все 6 класс! решить уравнение 3x-6(1+x)=-9x+9. выражение (b+1)^2-2b(3b+1). решить систему уравнений {8x-6y=6 под этим {-2x-6y=7. два острых угла прям треугольника относятся как 3 к 7 (3: 7) найдите большой острый угол ответ дайте в
градусах с объясением все)

Gdyxtk Gdyxtk    3   10.03.2019 13:50    1

Ответы
liliaseeee liliaseeee  06.06.2020 23:45

3x-6(1+x)=-9x+9

3x-6-6x=-9x+9

3x-6x+9x=9+6

6x=15

x=15/6

x=2.5

 

\left \{ {{8x-6y=6} \atop {-2x-6y=7}} \right.

Вычитаем из верхнего уравнения нижнее, второе уравнение оставляем без изменений

\left \{ {{8x-6y-(-2x-6y)=6-7} \atop {-2x-6y=7}} \right.

\left \{ {{8x-6y+2x+6y=-1} \atop {-2x-6y=7}} \right.

\left \{ {{10x=-1} \atop {-2x-6y=7}} \right.

\left \{ {{x=-\frac{1}{10}} \atop {-2x-6y=7}} \right.

Подставляем найденное неизвестное и находим второе неизвестное

\left \{ {{x=-\frac{1}{10}} \atop {-2*(-\frac{1}{10})-6y=7}} \right.

\left \{ {{x=-\frac{1}{10}} \atop {\frac{1}{5}-6y=7}} \right.

\left \{ {{x=-\frac{1}{10}} \atop {6y=\frac{1}{5}-7}} \right.

\left \{ {{x=-\frac{1}{10}} \atop {6y=-\frac{34}{5}}} \right.

\left \{ {{x=-\frac{1}{10}} \atop {y=-\frac{34}{5*6}}} \right.

\left \{ {{x=-\frac{1}{10}} \atop {y=-\frac{17}{15}}} \right.

\left \{ {{x=-\frac{1}{10}} \atop {y=-1\frac{2}{15}}} \right.

 

Задача

Обозначим один угол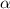 \alpha, другой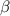 \beta

Составим пропорцию

\frac{\alpha}{\beta}=\frac{3}{7}

Из того, что треугольник прямоугольный следует, что

\alpha+\beta=90

Получили систему уравнений

\left \{ {{\frac{\alpha}{\beta}=\frac{3}{7}} \atop {\alpha+\beta=90}} \right.

Решаем

\left \{ {{\alpha=\frac{3}{7}*\beta} \atop {\alpha+\beta=90}} \right.

Подставляем

\left \{ {{\alpha=\frac{3}{7}*\beta} \atop {\frac{3}{7}*\beta+\beta=90}} \right.</p&#10;<p

\left \{ {{\alpha=\frac{3}{7}*\beta} \atop {\frac{10}{7}*\beta=90}} \right.

\left \{ {{\alpha=\frac{3}{7}*\beta} \atop {\beta=\frac{90*7}{10}}} \right.

\left \{ {{\alpha=\frac{3}{7}*\beta} \atop {\beta=63}} \right.

\left \{ {{\alpha=\frac{3}{7}*63} \atop {\beta=63}} \right.

\left \{ {{\alpha=27 \atop {\beta=63}} \right.

ответ: большой острый угол 63 градуса.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Vladimirmir28 Vladimirmir28  23.08.2019 15:50
X1+x2= -4 x1x2= -8 x1= x2= по теореме виета...
18Tanya 18Tanya  23.08.2019 15:50
8класс 1)2(х² +х-3)=5х²-6 2)(х+2)²+(х-2)²=3х²-9 3)6х²+9х -1=(2х+1)(2х-1) 4)4(х²-2)=х(1-х)-8 5)0,2х²-х(0,5х-1)=х-9 6)0,3х(х-4)+1,2х-2,7=2,7 7)3х(2х+3)=2х(х+4,5)+2 8)18-(х-5)(х-4)=...
1КрУтАя1 1КрУтАя1  23.08.2019 15:50
Мне нужно на завтра.постройте график функции у=х^2 . с графика определите: а) значение функции, соответствующее значению аргумента , равному 2,5 ; б) значение аргумента , при которых...
dover2 dover2  23.08.2019 15:50
Найдите радиус r описанной около треугольника abc окружности, если известно, что угол a=20 градусов, а=180...
kotelnikovsanya kotelnikovsanya  15.12.2020 12:19
Даны координаты вершины A( 3, -1) треугольника ABC и уравнения стороны BC: -9x + 6y + 15 = 0 и медианы BK: -15x + 8y + 35 = 0. Найти уравнение медианы AM....
alina20067 alina20067  15.12.2020 12:20
Представте в виде многочлена выражение (-2a+b^2)(2a+b^2)​...
anaradocina anaradocina  15.12.2020 12:20
Решить графически уравнение x2(во второй степени)=-3-4х...
zzzzzzz03 zzzzzzz03  15.12.2020 12:20
ответ должен быт девять пятых...
yakinaanna yakinaanna  12.05.2021 10:53
Найдите допустимые значение переменой 1)2х/х²-16​2)5х/х+1 + 3/х...
Настя20767 Настя20767  12.05.2021 10:53
Запишіть нравельну нерівність яка утворюється якщо до обох частин нерівності 8 12додати -7​...

Популярные вопросы