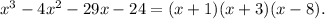Разложи на множители многочлен
Другие вопросы по теме Алгебра
Популярные вопросы
- Сочинение на тему кто в повести толстого детство является главный...
2 - Написать сочинение на тему я мечтаю стать врачом это моя мечта...
2 - Спиши , вставляя пропущенные буквы. прекрасный кипарис поднимался...
1 - Определи число, записанное римскими цифрами: mcxliii...
2 - Укажите слово, в морфемном составе которого есть суффикс д а)...
3 - До якої температури охолоне 5л окропу в каструлі віддавши в...
2 - Как определить существительное и прилагательное?...
2 - Вычислительная машина работает так: .*100+ . 1)запиши,какие...
1 - Нужно распределить на два столбика причастие и деепричастие....
3 - Цитаты из кавказского пленника толстова...
3
(x+1)(x-8)(x+3)
Объяснение:
x^3-4x^2-29x-24=x^3+x^2-5x^2-5x-24x-24=x^2(x+1)-5x(x+1)-24(x+1)=(x+1)(x^2-5x-24)=(x+1)(x^2-8x+3x-24)=(x+1)(x(x-8)+3(x-8))=(x+1)(x-8)(x+3)
Объяснение:
Для разложения многочлена на множители найдем его корни (напомним, что корнями многочлена называются числа, которые превращают его в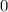 ).
).
Согласно следствию из теоремы Безу целые корни такого многочлена следует искать среди делителей свободного члена. Делителями числа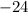 являются числа
являются числа 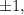
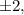
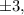
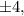
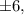
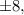
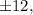
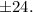 Последовательно начиная подставлять их в указанной последовательности, убеждаемся, что одним из корней данного многочлена является число
Последовательно начиная подставлять их в указанной последовательности, убеждаемся, что одним из корней данного многочлена является число 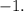 Это означает, что можно выделить линейный множитель, записав
Это означает, что можно выделить линейный множитель, записав 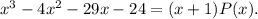
Для нахождения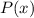 выполним деление
выполним деление 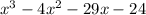 на
на 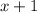 в столбик (см. рисунок). Получаем в частном квадратный трехчлен
в столбик (см. рисунок). Получаем в частном квадратный трехчлен 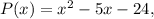 корни которого легко найти с теоремы Виета. Сумма корней должна быть равна
корни которого легко найти с теоремы Виета. Сумма корней должна быть равна 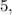 а их произведение —
а их произведение — 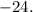 Легко подобрать такую пару чисел:
Легко подобрать такую пару чисел: 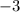 и
и 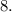 Тогда
Тогда 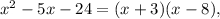 а исходный многочлен раскладывается на множители следующим :
а исходный многочлен раскладывается на множители следующим :