Пусть a и b - положительные числа. Найти 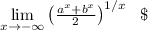 и
и 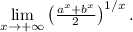
Другие вопросы по теме Алгебра
Популярные вопросы
- Найди точку графика линейной функции y=6x−2, абсцисса которой равна ординате....
1 - Склади усну розповідь на тему «Моя кімната», вико-ристовуючи іменники: кімната,...
2 - вставить правильно слова❤️...
1 - Привести 10 примеров присоединения уточняющих членов разными они предложены...
2 - Сергей потратил в книжном магазине 1237 руб. На покупку учебника он израсходовал...
2 - Художне означення називають...
2 - Английский,английский,английский,английский...
3 - Подумайте, насколько востребованы сегодня обычаи и традиции нашего народа...
1 - 1Wake up. 2walk. 3Go. Play. 4Watch. 5Go to bed. 6I am relaxing. 8planting.9doing....
3 - Ф.Искандера Тринадцатый подвиг Геракла . Назовите в рассказе все, что связано...
1
Объяснение:
b>a>0
Пусть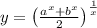 , тогда
, тогда
Значит
Аналогично со вторым номером
Пусть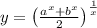 , тогда
, тогда
Значит