При каком наименьшем целом значении параметра a уравнение не имеет действительных корней: x^2 - (a - 6)x + 1/4 = 0
Другие вопросы по теме Алгебра
Популярные вопросы
- Монету подбрасывают 5 раз. Найти вероятность того, что герб выпадет ровно 2 раза...
1 - Студент в состоянии удовлетворительно ответить на 20 билетов из 25. Преподаватель...
1 - Сколькими можно выбрать карт одного цвета, а одну карту другого цвета среди шести...
3 - Опыт состоит в подбрасывании монеты до тех пор, пока два раза подряд она не выпадет...
2 - Вероятности попадания в цель при стрельбе из трех орудий таковы: р1=0,8 р2=0,7...
3 - Из партии изделий ОТК проверяет половину и признает годной всю партию, если среди...
3 - В мастерской два мотора работают независимо друг от друга. Вероятность того, что...
2 - Пластмассовые заготовки для деталей поступают с пресса №1, выпускающего 50% всей...
2 - По мишени производится 100 выстрелов. Каково наивероятнейшее число попаданий, если...
1 - Два стрелка независимо друг от друга по одному разу стреляют в мишень. Вероятность...
1
Квадратное уравнение не имеет корней среди действительных чисел тогда, и только тогда, когда его дискриминант отрицательный.
Дискриминант равен
Это парабола, которая отрицательна на промежутке
Единственное целое число в этом промежутке - 6.
Итого, ответ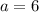 .
.
D<0
b^2-4ac<0
(-(a-6))^2-4*1/4<0
a^2-12a+36-1<0
a^2-12a+35<0
(a-7)(a-5)<0
+ - +
оо>
5 7 a
a придналежит (5;7). Наименьшим целым значением а, при котором начальное уравнение не имеет корней равно 6. 5 не подходит, ибо 5 не включается в решение неравестаа с параметром, а вот следущее целое число после пяти - это шесть.
ответ: 6