При каких значениях x значение производной функции f(x)=0

Объяснение:

23) f'(x) = 2x*e^(-x) + x^2*(-e^(-x)) = e^(-x)*(2x - x^2) = 0

x1 = 0; x2 = 2

24) f'(x) = 1/2 - (-1/2*sin(x/2)) = 1/2 + 1/2*sin(x/2) = 1/2*(1 + sin(x/2)) = 0

sin(x/2) = -1

x/2 = -П/2 + 2П*k

x = -П + 4П*k

25)

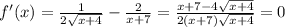
Область определения: x >= -4; x ≠ -7

x + 7 - 4√(x+4) = 0

x + 7 = 4√(x+4)

(x+7)^2 = 16(x+4)

x^2 + 14x + 49 = 16x + 64

x^2 - 2x - 15 = 0

(x - 5)(x + 3) = 0

x1 = -3; x2 = 5

26)

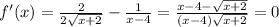
Область определения: x >= -2; x ≠ 4

x - 4 - √(x+2) = 0

x - 4 = √(x+2)

(x - 4)^2 = x + 2

x^2 - 8x + 16 = x + 2

x^2 - 9x + 14 = 0

(x - 2)(x - 7) = 0

x1 = 2; x2 = 7