При каких значениях переменной имеет смысл выражение:
1)
2)
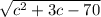
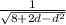
Другие вопросы по теме Алгебра
Популярные вопросы
- Какова главная мысль рассказа Саша и Шура...
3 - перший фонтан заповнює басейн за 2 години 30 хвилин, а другий за 3 години 45...
2 - Определите, в каком месте - до или после водорода - в ряду активности находится...
2 - Алёна масла таямницы закинутой хаты, краткое содержание главные герои...
1 - Что тебя заинтересовало в повести Белкина?? о чем заставила задуматься??...
3 - Нужно краткое содержание на 5 предложений-Повести «Детство»Толстой, но не из...
3 - Какое стихотворение самое длинное? Давайте так , я за ответ на вопрос а тот...
3 - Как готовиться к ОГЭ по биологии с нуля??...
2 - Найти решение уровненияна промежутке (-2;1). ответ с об яснением...
3 - Дайте ответ на этот вопрос мне это важно...
1
Объяснение:
Найдём нули функции:
Найдём нули функции: