Постройте график функции y=|x^2 +х – 2|. какое наибольшее число
общих точек может иметь график данной функции с прямой,
параллельной оси абсцисс? ​

ответ: 4.

Объяснение: Для начала построим график функции y = x² + x - 2

ординаты вершины: ,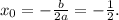

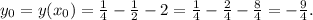
Координаты точек пересечения с осями координат:

1) с ОХ: у = 0. x² + x - 2 = 0. По теореме Виета х₁ = 1, х₂ = -2.  (1; 0), (-2; 0)

2) с ОУ: х = 0. у(0) = 0 + 0 - 2 = -2.  (0; -2).

График - во вложении 1.

Из графика y = x² + x - 2 можно получить график функции y = |x² + x - 2|, если ту часть графика, которая ниже оси ОХ, "отзеркалить" относительно оси ОХ. В итоге получим график во вложении 2.

Прямая, параллельная оси абсцисс, имеет вид y = a, где а - произвольное число. Будем подбирать разные значения параметра а и посмотрим, какое максимальное кол-во общих точек будут иметь наша функция и прямая y = a. (вложение 3)

Если а < 0 (наглядный пример - а = -0,4), то общих точек не будет вообще.

Если а = 0 (прямая совпадает с осью ОХ), то имеем ровно две точки пересечения.

Если а = 9/4 (отзеркаленная вершина), то иметь будем 3 точки пересечения. А если брать промежуточные значения - 0 < a < 9/4 (наглядный пример - а = 1,5), - то будет 4 точки пересечения, т.е. 4 общих точки.

Если брать значения а > 9/4 (наглядный пример - а = 3), то у нас будет только 2 общих точки.

Итого: наибольшее число общих точек графиков наших функций - 4.